راکتانس خازنی 

راکتانس

راکتانس خازنی، امپدانس پیچیده خازنی است که مقدار آن با توجه به فرکانس اعمال شده تغییر می‌کند.

در آموزش شبکه RC دیدیم که وقتی یک ولتاژ DC به یک خازن اعمال می شود، خازن خودش یک جریان شارژ را از منبع تغذیه می‌کشد و تا بالا و مقدار برابر با ولتاژ اعمال شده شارژ می‌کند.

راکتانس خازنی

هنگامی که ولتاژ منبع تغذیه کاهش می‌یابد، شارژ ذخیره شده در خازن نیز کاهش می یابد و خازن تخلیه می شود. اما در یک مدار AC ، سیگنال ولتاژ اعمال شده به طور پیوسته از یک قطب مثبت به یک قطب منفی در سرعت تعیین شده توسط فرکانس منبع تغذیه تغییر می‌کند، به عنوان مثال در مورد ولتاژ موج سینوسی، به عنوان مثال، خازن به طور مداوم با نرخ تعیین شده توسط فرکانس تغذیه، شارژ یا تخلیه می شود.

هنگامی که خازن شارژ یا تخلیه می‌شود، جریانی که از آن جریان می یابد توسط امپدانس داخلی خازن محدود می شود. این امپدانس داخلی معمولاً با عنوان راکتانس خازنی شناخته می شود و نماد X_C در اهم به آن داده می شود.

برخلاف مقاومت که دارای یک مقدار ثابت است، به عنوان مثال 100Ω ، 1kΩ ، [latex] 10kOmega [/latex] و غیره، (این به این دلیل است که مقاومت از قانون اهم پیروی می کند)، راکتانس خازنی با فرکانس اعمال شده تغییر می‌کند، بنابراین هرگونه تغییر در فرکانس تغذیه تأثیر زیادی بر مقدار “راکتانس خازنی” خازن می‌گذارد.

فرمول راکتانس خازنی

با افزایش فرکانس بکار رفته در خازن، راکتانس آن کاهش می‌یابد (در اهم اندازه گیری می شود). به همین ترتیب با افزایش فرکانس دو سر خازن، مقدار راکتانس آن افزایش می یابد. این تغییر،  امپدانس پیچیده خازن نامیده می‌شود.

امپدانس پیچیده وجود دارد زیرا الکترون ها در حالت بار الکتریکی روی صفحات خازن، با توجه به  فرکانس متغیر، به نظر می‌رسد که با سرعت بیشتری از یک صفحه به صفحه دیگر منتقل می شوند.

با افزایش فرکانس، خازن در مدت معینی شارژ بیشتری را در صفحاتش منتقل می کند و در نتیجه جریان بیشتری در خازن جریان می‌یابد  و انگار که امپدانس داخلی خازن کاهش یافته است. بنابراین، یک خازن متصل به مدار که در محدوده مشخصی از فرکانس ها تغییر می کند می توان گفت که “وابسته به فرکانس” است.

 راکتانس خازنی دارای نماد الکتریکی “X_C” است و دارای واحدهایی است که همانند مقاومت (R) در اهم اندازه گیری شده است. آن با استفاده از فرمول زیر محاسبه می شود:

فرمول راکتانس خازنی : [latex] X_{c}=(frac{1}{2Pi fc}) [/latex]

بطوریکه:

Xc = راکتانس خازنی در اهم، (Ω)

π (pi) = 3.142 (اعشاری) یا به صورت 7/ 22 (کسری)

ƒ = فرکانس در هرتز ، (Hz)

C = ظرفیت در فاراد ، (F)

مثال شماره 1 راکتانس خازنی

مقدارراکتانس خازنی با مقدار 220 نانومتر را در فرکانس [latex] 1KHz [/latex] و دوباره در فرکانس 20kHz  را محاسبه کنید.

در فرکانس [latex] 1KHz [/latex]:

[latex] X_{c}=(frac{1}{2Pi fc})=(frac{1}{2Pi times 1000times 220times 10^{-9}})=723.4Omega [/latex]

دوباره در فرکانس 20kHz :

[latex] X_{c}=(frac{1}{2Pi fc})=(frac{1}{2Pi times 20000times 220times 10^{-9}})=36.2Omega [/latex]

بطویکه f فرکانس در هرتز و C ظرفیت خازن در فاراد است.

بنابراین، از بالا مشاهده می شود که با افزایش فرکانس اعمال شده در دو سر خازن 220 نانومتر، از kHz1 به 20kHz، مقدار راکتانس آن X_C کاهش می یابد، از تقریباً [latex] 723Omega [/latex]  به 36Ω می رسد و این همیشه به عنوان راکتانس خازنی  X_C  درست است و بصورت معکوس با  فرکانس متناسب است و جریان منتقل شده توسط خازن برای یک ولتاژ معین متناسب با فرکانس است.

برای هر مقدار داده شده از ظرفیت خازن، راکتانس یک خازن X_C بیان شده در اهم می تواند نسبت به فرکانس مطابق شکل زیر رسم شود.

راکتانس خازنی نسبت به فرکانس

با تنظیم مجدد فرمول راکتانس فوق، می توانیم دریابیم که در چه فرکانسی یک خازن مقدار راکتانس خازنی خاصی (X_C) را خواهد داشت.

مثال شماره 2 راکتانس خازنی

در کدام فرکانس خازن 2/2 میکرو فاراد، دارای یک مقدار فرکانس 200 اهم است؟

[latex] X_{c}=(frac{1}{2Pi CX_{c}})=(frac{1}{2Pi times 2.2times 200times 10^{-6}})=361.7Hz [/latex]

یا می توانیم با دانستن فرکانس اعمال شده و مقدار راکتانس آن در آن فرکانس، مقدار خازن را در فاراد بیابیم.

مثال شماره 3 راکتانس خازنی

هنگامی که راکتانس خازنی  200Ω است و آن به یک تغذیه Hz 50 وصل شده است مقدار ظرفیت خازن در فاراد چقدر خواهد بود.

[latex] X_{c}=(frac{1}{2Pi fX_{c}})=(frac{1}{2Pi times 50times 200 })=15.92mu F [/latex]

از مثالهای فوق می توان دریافت که یک خازن وقتی به منبع فرکانس متغیر متصل است، کمی شبیه به “مقاومت متغیر کنترل شده با فرکانس” عمل می‌کند، زیرا راکتانس آن (X) به طور مستقیم متناسب با فرکانس است. در فرکانسهای بسیار کم، مانند خازن 1 هرتز، خازن 220 نانومتری ما دارای مقدار راکتانس خازنی بالایی در حدود [latex] 3.723KOmega [/latex]  (اثر یک مدار باز را می‌دهد) است.

در فرکانس های بسیار بالا مانند 1 مگاهرتز خازن دارای مقدار راکتانس خازنی کم فقط 0.72Ω است (اثر مدار اتصال کوتاه را می‌دهد). بنابراین در فرکانس صفر یا حالت پایدار DC خازن 220 نانومتری ما دارای راکتانس  بی نهایت است که بیشتر شبیه یک “مدار باز” بین صفحات است و هر جریانی که از آن می‌گذرد را مسدود می کند.

مرور تقسیم ولتاژ

ما از آموزش خود در مورد مقاومت ها در سری به خاطر می‌آوریم که بسته به مقدار مقاومت، ولتاژهای مختلفی در دو سر هر مقاومت می‌تواند دیده شود و یک مدار تقسیم کننده ولتاژ توانایی تقسیم ولتاژ تغذیه خود با نسبت [latex] R_{2}/R_{1}+R_{2} [/latex] را دارد. بنابراین، وقتی R₁ = R₂ ولتاژ خروجی نصف مقدار ولتاژ ورودی خواهد بود. به همین ترتیب، هر مقدار R₂ بزرگتر یا کمتر از R₁ منجر به تغییر متناسب با ولتاژ خروجی خواهد شد. مدار زیر را در نظر بگیرید.

شبکه تقسیم کننده ولتاژ

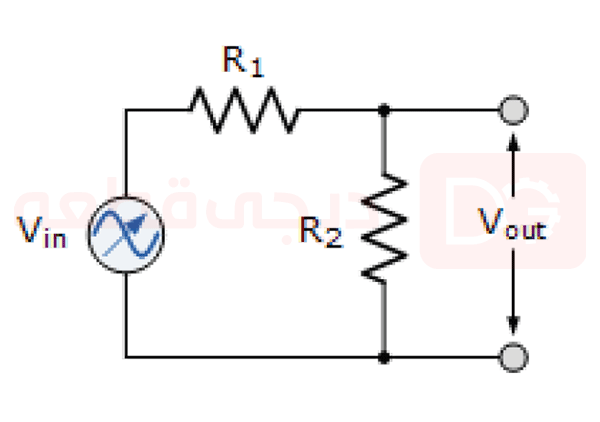
[latex] V_{out}=V_{in}(frac{R_{2}}{R_{1}+R_{2}}) [/latex]

اکنون می دانیم که مقدار راکتانس خازنیX_C   (امپدانس پیچیده آن) با توجه به فرکانس اعمال شده تغییر می کند. اگر اکنون مقاومت R₂ فوق را برای خازن تغییر دهیم، با تغییر فرکانس، افت ولتاژ در دو مؤلفه تغییر می کند زیرا راکتانس خازن روی امپدانس آن تأثیر می گذارد.

امپدانس مقاومت R₁ با فرکانس تغییر نمی کند. مقاومت ها دارای مقادیر ثابت هستند و از تغییر فرکانس بی تاثیر می‌مانند. سپس ولتاژ دوسر مقاومت R₁ و بنابراین ولتاژ خروجی با راکتانس متناوب خازن در فرکانس معین مشخص شده است. این منجر به یک مدار تقسیم ولتاژ RC وابسته به فرکانس می شود. با در نظر گرفتن این ایده، فیلترهای پایین گذر و بالا گذر منفعل با جایگزینی یکی از مقاومتهای تقسیم ولتاژ با خازن مناسب همانطور که نشان داده شده است، می‌توانند ساخته شوند.

فیلتر پایین گذر

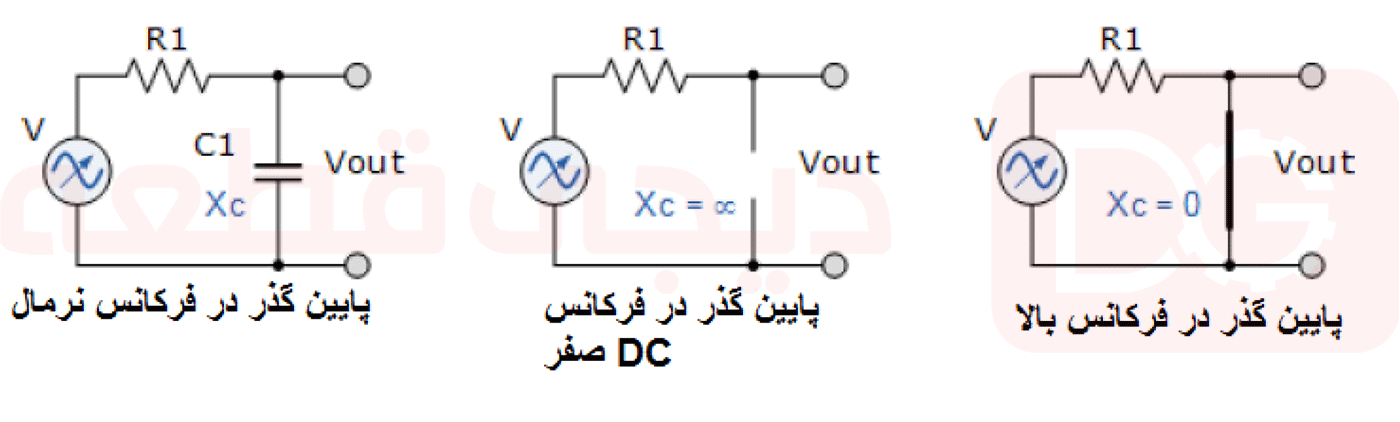
فیلتر بالا گذر

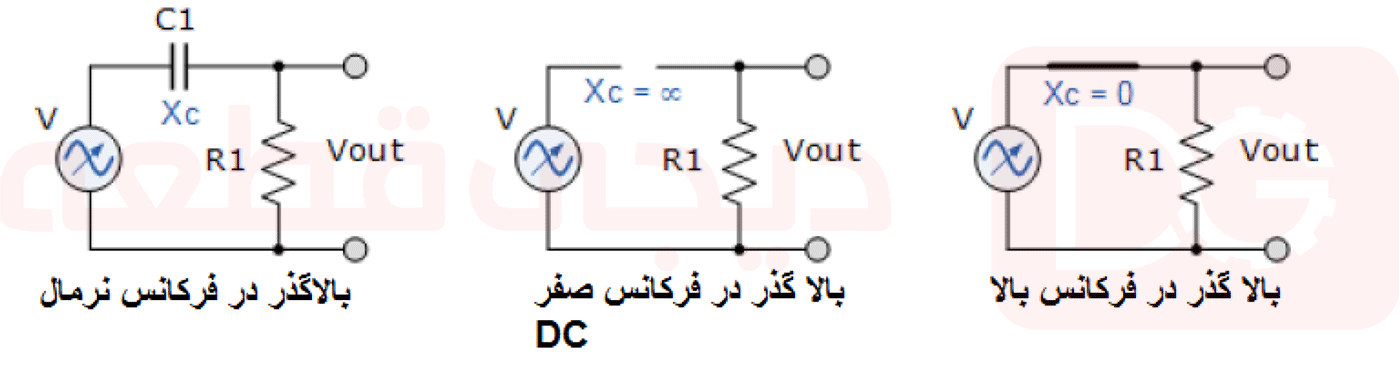
خاصیت راکتانس خازنی، باعث می شود تا خازن برای استفاده در مدارهای فیلتر AC یا در مدارهای هموار کننده منبع تغذیه DC، ایده آل باشد تا اثرات هرگونه ولتاژ موج ناخواسته را کاهش دهد. زیرا خازن یک مسیر سیگنال مداری کوتاه را برای هر سیگنال فرکانس ناخواسته در ترمینالهای خروجی  اعمال می‌کند.

خلاصه واکنش خازنی

بنابراین، ما می توانیم رفتار یک خازن را در یک مدار متغیر فرکانسی به عنوان نوعی مقاومت کنترل شده با فرکانس که دارای یک مقدار راکتانس خازنی بالا (شرایط مدار باز) در فرکانسهای بسیارکم و مقدار راکتانس خازنی پایین (شرط اتصال کوتاه) در فرکانس های خیلی بالا است، خلاصه کنیم که در نمودار بالا نشان داده شده است.

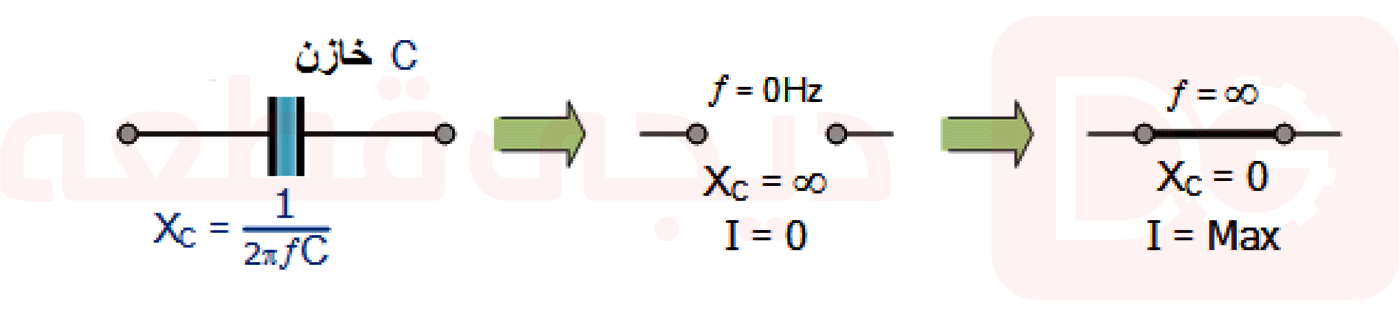
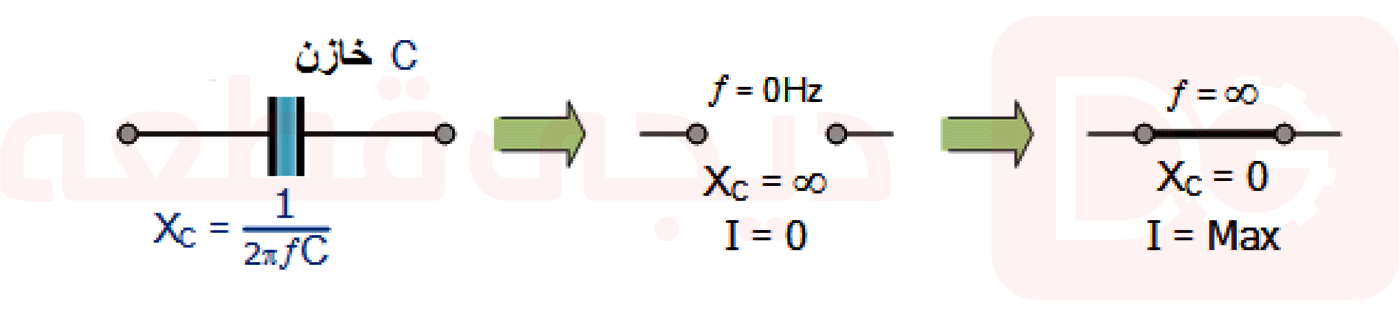
خیلی مهم است تا این دو شرایط را بخاطر بسپاریم  و در آموزش بعدی ما در مورد فیلتر پایین گذر منفعل، به استفاده از راکتانس خازنی خواهیم پرداخت تا هرگونه سیگنال فرکانس بالا ناخواسته را مسدود کنیم در حالی که فقط به سیگنالهای فرکانس پایین اجازه  عبور داده می‌شود.