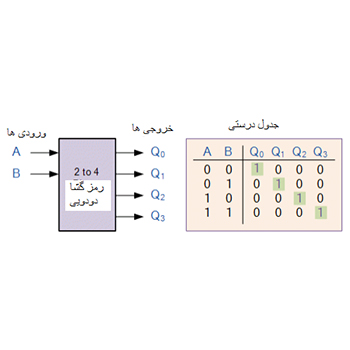
رمز گشا دودویی 

رمز گشا دودویی مدار منطقی ترکیبی ساخته شده دیگری از گیت‌های منطقی مستقل است و دقیقا مخالف با یک رمز نگار است.

رمز گشا دودویی

نام “رمزگشای” به معنی ترجمه یا رمزگشایی اطلاعات کد شده از یک قالب به قالب دیگر است، بنابراین یک رمزگشای باینری با استفاده از خروجی‌های “n)، “2n) سیگنال‌های ورودی باینری را به یک کد معادل تبدیل می‌کند.

رمزگشاهای باینری نوع دیگری از قطعات منطقی دیجیتال هستند که بسته به تعداد خطوط ورودی داده، کدهای 2 بیتی ، 3 بیتی یا 4 بیتی دارد، بنابراین رمزگشایی که دارای دو یا چند بیت مجموعه باشد، به صورت زیر تعریف می‌شود:

                                                      داشتن یک کد n-بیتی ، بنابراین امکان نمایش2ⁿ

مقادیر ممکن وجود دارد. بنابراین، یک رمزگشا با تنظیم دقیقاً یکی از n خروجی‌های خود، بر اساس منطق “1” یک مقدار دودویی را به مقدار غیر دودویی رمزگشایی می‌کند.

اگر یک رمزگشا باینری n ورودی را دریافت کند (که معمولاً به صورت یک عدد باینری یا بولی گروه بندی می‌شود) بر اساس آن ورودی، آن یک و تنها یکی از 2ⁿ خروجی خود را با غیرفعال شدن دیگر خروجی‌ها فعال می‌کند.

به عنوان مثال، یک مبدل (NOT-گیت) را می توان به عنوان یک دریافت کننده باینری 1 به 2 طبقه بندی کرد: 1 ورودی و 2 خروجی (2¹) امکان پذیر است زیرا با یک ورودی A می تواند دو خروجی A و  تولید کند ( not-A) که نشان داده شده است.

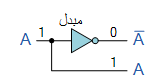
سپس می‌توان گفت که یک رمزگشای منطقی ترکیبی استاندارد یک رمزگشای n به m است ، که در آن m ≤ 2n ، و خروجی آن Q فقط به حالات ورودی فعلی آن وابسته است. به عبارت دیگر، یک رمزگشا باینری به ورودی‌های فعلی خود نگاه می کند، تعیین می‌کند کد دودویی یا تعداد دودویی در ورودی‌های آن چیست و خروجی مناسب متناسب با آن ورودی باینری را انتخاب می‌کند.

رمزگشای باینری ورودی‌های رمزگذاری شده را به خروجی‌های رمزگذاری شده تبدیل می‌کند، جایی که کدهای ورودی و خروجی متفاوت هستند و رمزگشاها برای رمزگشایی یا الگوی ورودی باینری یا BCD (کد 8421) به یک کد خروجی ده دهی در دسترس هستند. رمزگشاهای BCD به اعشاری که معمولاً در دسترس هستند شامل TTL 7442 یا CMOS 4028 هستند. به طور کلی کد خروجی رمزگشاها بیت بیشتری نسبت به کد ورودی آن دارد و مدارهای عملی “رمزگشای باینری” شامل پیکربندی های خط 2 به 4 ، 3 به 8 و 4 به 16 است.

رمز گشا 2 به 4 دودویی

مثالی از رمزگشای خطی 2 به 4 به همراه جدول درستی آن به صورت زیر آورده شده است:

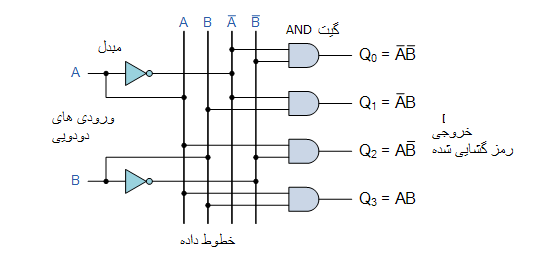
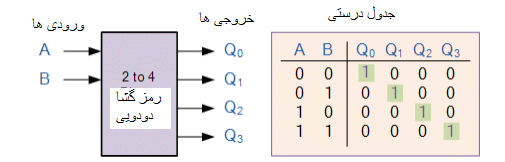
این مثال ساده بالا در مورد رمزگشای باینری 2 تا 4 خطی از یک آرایه چهار گیتی AND تشکیل شده است. 2 ورودی باینری با برچسب A و B در یکی از 4 خروجی رمزگشایی می شوند، از این رو شرح رمزگشای باینری 2 به 4 است. هر خروجی نشان دهنده یکی از مینی اصطلاح  متغیر 2 ورودی است (هر خروجی = یک مینی اصطلاح).

ورودی‌های باینری A و B تعیین می‌کنند که کدام خط خروجی از Q0 تا Q3 در سطح منطقی “1” “بالا” است در حالی که خروجی های باقی مانده در منطق “0” “پایین” نگه داشته می شوند بنابراین فقط یک خروجی می‌تواند در هر زمان فعال باشد (بالا). بنابراین، هر کدام از خطهای خروجی که “بالا” باشد کد باینری موجود در ورودی را مشخص می‌کند، به عبارت دیگر ورودی دودویی را “رمزگذاری” نمی‌کند.

برخی از رمزگشاهای باینری دارای یک پین ورودی اضافی با عنوان “فعال کردن” هستند که خروجی‌های دستگاه را کنترل می‌کند. این ورودی اضافی اجازه می‌دهد تا خروجی رمزگشاها در صورت لزوم “روشن” یا “خاموش” شوند. این نوع رمزگشاهای باینری معمولاً به عنوان “رمزگشای آدرس حافظه” در برنامه‌های حافظه ریز پردازنده استفاده می‌شوند.

می‌توان گفت که یک رمزگشا باینری یک مولتی پلکسر با یک خط داده اضافی است که برای فعال کردن رمزگشا استفاده می‌شود. یک روش جایگزین برای مشاهده مدار رمزگشا، در نظر گرفتن ورودی های A ، B و C به عنوان سیگنال‌های آدرس است. هر ترکیبی از A ، B یا C یک آدرس حافظه منحصر به فرد را تعریف می‌کند.

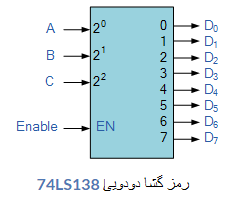
ما دیده ایم که برای رمزگشایی هر کد باینری 2 بیتی می‌توان از رمزگشای باینری 2 به 4 خط (TTL 74155) برای ارائه چهار خروجی، برای هر ترکیب ورودی احتمالی ، یک خروجی استفاده کرد. با این حال، گاهی اوقات نیاز به داشتن یک رمزگشای باینری با تعدادی خروجی بیشتر از مقدار موجود است، بنابراین با اضافه کردن ورودی‌های بیشتر، رمزگشا می‌تواند به طور بالقوه 2ⁿ خروجی بیشتر فراهم کند.

بنابراین به عنوان مثال، یک رمزگشا با 3 ورودی باینری (3 = n) ، یک رمزگشای خطی 3 به 8 (TTL 74138) و 4 ورودی (4 = n) یک رمزگشای خطی 4 به 16 ( 7477 TTL) تولید می‌کند و غیره اما یک رمزگشا همچنین می‌تواند کمتر از 2ⁿ خروجی داشته باشد مانند رمزگشا BCD به رمزگشا نمایشگر هفت بخشی (TTL 7447) که دارای 4 ورودی و تنها 7 خروجی فعال برای هدایت یک صفحه نمایش است تا 16 (2⁴) خروجی کامل همانطور که انتظار دارید، راه اندازی کند.

در اینجا رمزگشای باینری 4 (3 داده به علاوه 1 فعال) به 16 خط بسیار بزرگتر با استفاده از دو رمزگشا کوچکتر 3 به 8 اجرا شده است.

پیکربندی رمز گشا دودویی 4 به 16

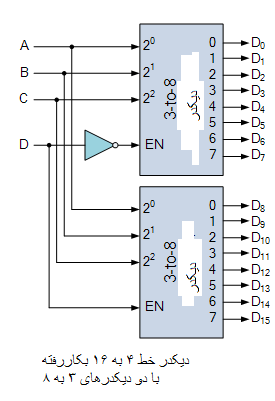
از ورودی های A ، B ، C برای انتخاب خروجی در هر رمزگشا با منطق “1” (HIGH) استفاده می‌شود و از ورودی D با ورودی فعال برای انتخاب کدگذار یا اولین یا دوم با خروجی “1” استفاده می‌شود.

با این حال، تعداد ورودی‌هایی که می توانند برای یک رمزگشا خاص استفاده شوند محدودیت دارد، زیرا با افزایش n ، تعداد گیت هایAND مورد نیاز برای تولید یک خروجی نیز بزرگتر می شود و منجر به بزرگ شدن گیت‌های مورد استفاده برای راه اندازی آنها می‌شود.

این نوع رمزگشای فعال “بالا” فقط با استفاده از اینورترها، (نه گیت ها) و گیت‌های AND قابل اجرا است. استفاده از گیت AND به عنوان عنصر اصلی رمزگشایی برای خروجی راحت است زیرا تنها درصورتی که تمام ورودی‌های آن منطقی “1” باشد ، یک خروجی “بالا” یا “1” منطقی تولید می‌کند.

اما برخی از دیکدرهای باینری با استفاده از گیت های NAND به جای گیت AND برای خروجی رمزگشایی شده ساخته می‌شوند، زیرا تولید گیت‌های NAND ارزان تر از AND است زیرا برای اجرای آنها ترانزیستورهای کمتری در نظر گرفته شده است.

استفاده از گیت‌های NAND به عنوان عنصر رمزگشایی، منجر به خروجی فعال “LOW” می‌شود در حالی که بقیه “HIGH” خواهد بود. همانطور که یک گیت NAND عملیات AND را با یک خروجی معکوس تولید می‌کند، رمزگشای NAND با جدول درستی معکوس خود به این شکل است.

رمز گشا دودویی NAND دو به چهار خطی

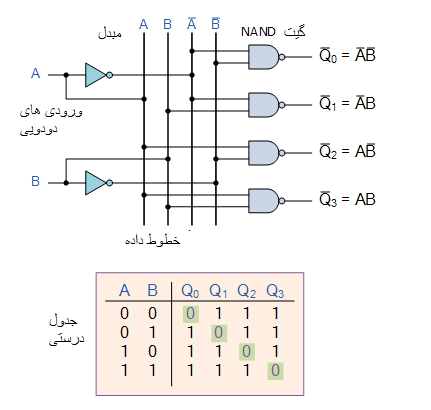
سپس برای رمزگشای NAND ، فقط یک خروجی می‌تواند پایین و برابر با منطق “0” در هر زمان باشد، با این که تمام خروجی‌های دیگر در منطق “1” بالا هستند.

رمزگشاها همچنین با یک پین ورودی اضافی “فعال” در دسترس هستند که به شما اجازه می‌دهد خروجی رمزگشایی شده “به” روشن یا “خاموش” با استفاده از منطق “1” یا منطق “0” به ترتیب بر روی آن تغییر یابد. بنابراین به عنوان مثال، وقتی ورودی فعال در سطح منطقی “0” باشد ، (EN = 0) همه خروجی‌ها در منطق “0” (برای گیت های AND) بدون در نظر گرفتن وضعیت ورودی‌های A و B “خاموش” هستند.

به طور کلی برای اجرای این عملکرد امکان پذیر، گیت‌های 2 ورودی AND و یا NAND با گیت های 3 ورودی AND یا NAND جایگزین می‌شوند. پین ورودی اضافی عملکرد فعال را نشان می‌دهد.

رمزگشای آدرس حافظه

رمزگشاهای باینری اغلب در سیستم های دیجیتالی پیچیده تر برای دسترسی به یک مکان حافظه خاص بر اساس “آدرس” تولید شده توسط یک دستگاه محاسباتی استفاده می‌شوند. در سیستم‌های ریزپردازنده مدرن، میزان حافظه مورد نیاز می‌تواند بسیار زیاد باشد و به طور کلی بیش از یک تراشه حافظه منفرد است.

یک روش برای غلبه بر این مشکل اتصال بسیاری از تراشه‌های حافظه جداگانه به یکدیگر و خواندن داده ها در یک “گذرگاه اطلاعات” مشترک است. به منظور جلوگیری از “خواندن” داده‌ها از هر تراشه حافظه به طور همزمان، هر تراشه حافظه به طور جداگانه و همزمان انتخاب می‌شود و این فرآیند به عنوان رمزگشایی آدرس شناخته می‌شود.

در این نوع برنامه‌ها، آدرس ورودی داده رمزگذاری شده را نشان می‌دهد و خروجی‌ها سیگنال‌های انتخاب عنصر حافظه خاص هستند. هر تراشه حافظه دارای ورودی به نام انتخاب  Chip یا CS است که توسط MPU (واحد میکرو پردازنده) برای انتخاب تراشه حافظه مناسب در صورت لزوم استفاده می‌شود. به طور کلی یک منطق “1” در ورودی تراشه (CS) ورودی حافظه را انتخاب می‌کند در حالی که منطق “0” در ورودی آن را انتخاب همزمان می‌کند.

بنابراین با انتخاب یا انتخاب همزمان هر تراشه، می توانید قطعه آدرس حافظه صحیح را برای یک مکان آدرس خاص انتخاب کنیم. مزیت رمزگشایی آدرس این است که وقتی آدرس حافظه خاصی را مشخص می‌کنیم، محل حافظه مربوطه فقط در یکی از تراشه‌ها وجود دارد.

به عنوان مثال بیایید فرض می‌کنیم که ما یک سیستم ریزپردازنده بسیار ساده داریم که فقط 1 کیلوبایت (یک هزار بایت) حافظه RAM و 10 خط آدرس حافظه در دسترس دارد. حافظه از دستگاه های 128 × 8 بیتی (128 × 8 = 1024 بایت) تشکیل شده است و برای Kb 1 به 8 تراشه حافظه جداگانه نیاز داریم اما برای انتخاب تراشه حافظه صحیح به رمزگشای باینری 3 تا 8 خطی نیز نیاز داریم که در زیر نشان داده شده است.

رمز گشایی آدرس حافظه

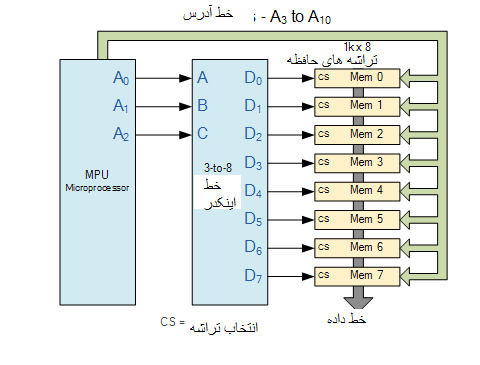
رمزگشای باینری برای انتخاب هر یک از 8 تراشه (قسمت پایین آدرس) فقط به 3 خط آدرس نیاز دارد (A0 تا A2) ، در حالی که 8 خط آدرس باقی مانده (A3 تا A10) مکان حافظه صحیح را روی آن تراشه انتخاب می‌کنند (قسمت بالای آدرس).

با انتخاب محل حافظه با استفاده از گذرگاه آدرس، اطلاعات مربوط به محل حافظه داخلی خاص برای استفاده توسط ریز پردازنده به یک “گذرگاه داده” مشترک ارسال می‌شود. این البته یک مثال ساده است اما اصول اصلی برای انواع تراشه‌ها یا ماژول‌های حافظه یکسان است.

رمزگشاهای دودویی قطعات بسیار مفیدی برای تبدیل یک قالب دیجیتال به فرمت دیگر هستند، مانند داده‌های باینری یا نوع BCD به اعشاری یا اکتال و غیره و آی سی های رمزگشا دیجیتال رایج در دسترس رمزگشا دودویی خط 3 به 8 TTL 74LS138 یا 74ALS154 4 هستند. آنها همچنین برای ارتباط با نمایشگرهایی مانند TTL 74LS47 که در آموزش بعدی بررسی خواهیم کرد بسیار مفید هستند.