آشنایی با مقاومت های موازی 

مقاومت های موازی با یکدیگر بصورت موازی بسته شده‌اند. هنگامی که هر دو پایانه آنها متناظرا با هر پایانه مقاومت یا مقاومت‌های دیگر وصل شود.

مقاومت موازی

برخلاف مدار مقاومتی سری قبلی، در شبکه مقاومت های موازی از آنجا که چند مسیر برای جاری شدن جریان وجود دارد جریان مدار می‌تواند بیش از یک مسیر برگزیند. مدارهای موازی بصورت تقسیم‌کننده‌های جریان طبقه‌بندی شده‌اند.

از آنجا که چند مسیر برای جاری شدن جریان تغذیه وجود دارد، جریان ممکن است برابر با جریانی که در شاخه‌های شبکه موازی جاری می‌شود، نباشد. اگرچه، افت ولتاژ دو سر تمام مقاومت‌ها در شبکه مقاومتی موازی یکسان است. سپس، مقاومت های موازی، ولتاژ مشترک در دوسر خود دارند و این برای تمام مولفه‌های متصل شده بصورت موازی صحیح است.

بنابراین می‌توان یک مدار مقاومتی موازی را بصورتی که مقاومت‌ها به دو نقطه (یا گره) یکسان وصل شده‌اند که بیش از یک مسیر جریان متصل به یک منبع ولتاژ مشترک وجود دارد تعریف کرد. سپس در مثال مقاومت های موازی زیر ولتاژ دو سر مقاومت R1 معادل با ولتاژ دو سر مقامت R2 که معادل با ولتاژ دو سر R3 که همگی معادل با ولتاژ تغذیه هستند، است. درنتیجه، برای یک شبکه مقاومت موازی این بصورت زیر تعریف شده است:

در مقاومت‌های ذکر شده در مدار موازی مقاومت‌های R1 ,R2 و R3 همگی بصورت موازی بین دو نقطه A و B وصل شده‌اند که در زیر نشان داده شده است.

مدار مقاومت های موازی

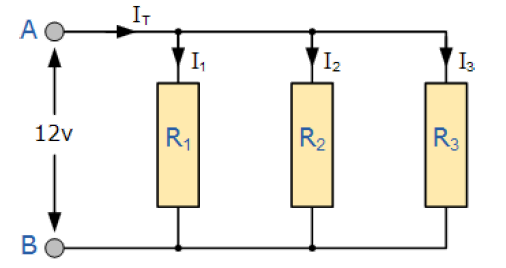
در شبکه مقاومت سری قبلی، دیدیم که مقاومت کلی R_T مدار برابر با مجموع تمام مقاومت‌های اضافه شده به یکدیگر بود. برای مقاومت های موازی، مقاومت مدار معادل R_T بصورت متفاوت محاسبه می‌شود.

اینجا، به جای اینکه عکس مجموع جبری مقاومت‌ها معادل با مقاومت معادل باشد، عکس(1/R) مقدار مقاومت‌های مستقل همگی به یکدیگر معادل با مقاومت معادل می‌شود، که نشان داده شده است.

رابطه مقاومت های موازی

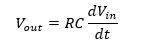
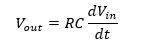
 سپس معکوس مقاومت معادل دو یا چند مقاومت متصل بصورت موازی جمع جبری معکوس مقاومت‌های مستقل است.

اگر دو مقاومت یا امپدانس‌های موازی برابر و مقدار یکسان داشته باشند، سپس مقاومت کلی یا معادل R_T معادل با نصف مقدار یک مقاومت می‌شود. آن برابر با R/2 و برای سه مقاومت یکسان بصورت موازی، R/3 است.

توجه داشته باشید که مقاومت معادل همیشه کمتر از کوچکترین مقاومت در شبکه موازی است، و بنابراین مقاومت کلی R_T همیشه با اضافه شدن مقاومت های موازی اضافی کاهش خواهد یافت.

مقاومت های موازی به ما مقدار به عنوان کنداکتانس، با نماد G با واحد سیمنس با نماد S ارائه می‌دهد. کنداکتانس کسر یا معکوس مقاومت (G=1/R) است. برای تبدیل کنداکتانس به عقب به یک مقدار مقاومت نیاز داریم تا مقدار کنداکتانس داده شده را عکس کنیم سپس مقاومت کلی R_T بدست می‌آید.

اکنون می‌دانیم که مقاومت‌هایی که بین دو نقطه یکسان وصل شده‌اند بصورت موازی هستند. اما یک مدار مقاومت موازی شکل‌های بسیاری جدای از آنچه در بالا نشان داده شد دارد و اینجا چند نمونه از اینکه مقاومت‌ها چگونه بصورت موازی به یکدیگر وصل می‌شوند ارائه شده است.

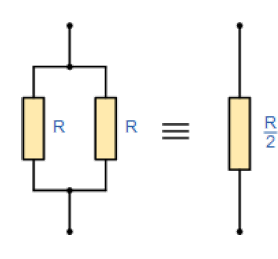
شبکه‌ های مقاومت موازی گوناگون

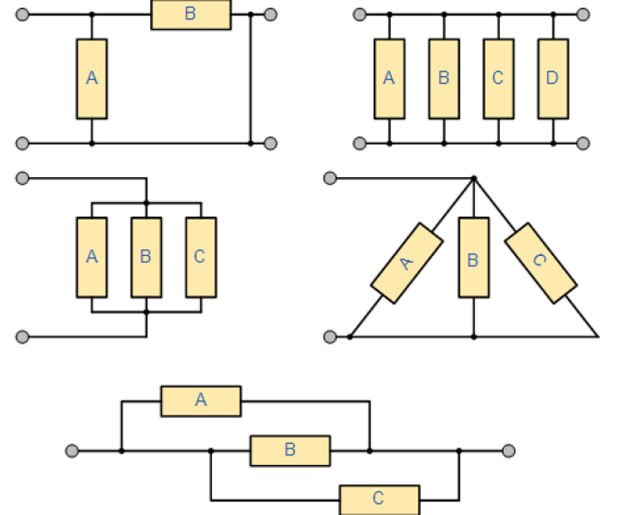
5 شبکه مقاومتی فوق ممکن است متفاوت از یکدیگر دیده شوند، اما آنها همگی بصورت مقاومت های موازی مرتب شده‌اند و موقعیت و روابط یکسان بر آنها اعمال شده است.

مثال شماره 1 برای مقاومت های موازی

مقاومت کلی R_T، مقاومت‌های زیر که در شبکه موازی به یکدیگر وصل شده‌اند را بیابید.

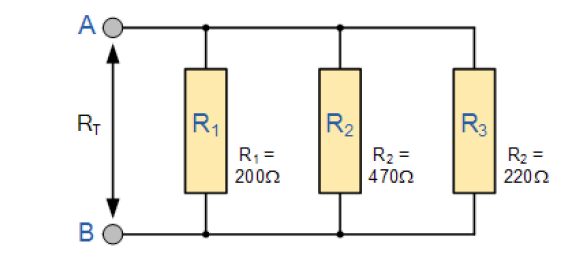
مقاومت کلی R_T دو سر ترمینال A و B بصورت زیر محاسبه شده است:

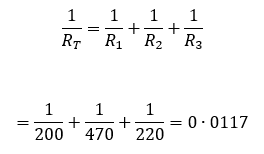
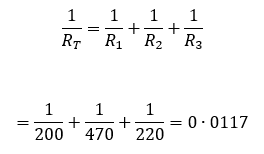
درنتیجه:

این متد محاسبات عکس می‌تواند برای محاسبه‌کردن هر تعداد مقاومت‌های مستقل متصل به یکدیگر در داخل یک شبکه موازی واحد استفاده شود.

اگرچه، تنها دو مقاومت مستقل موازی وجود دارد سپس می‌توانیم فرمول سریعتر برای یافتن مقدار مقاومت معادل یا مجموع R_T بکار ببریم و کمی در کاهش پیچیدگی روابط ریاضی کمک نماییم.

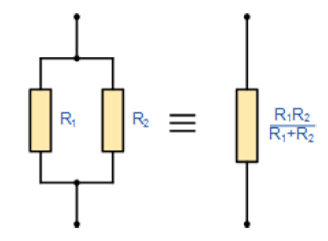
این روش بسیار سریع ضرب بر روی جمع برای محاسبه دو مقاومت به طور موازی، با مقادیر مساوی یا نابرابر به شرح زیر است:

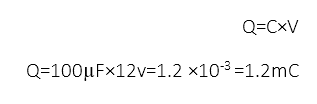
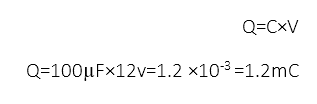
مثال شماره 2 مقاومت موازی

مدار زیر که دارای تنها دو مقاومت در ترکیب موازی است در نظر بگیرید:

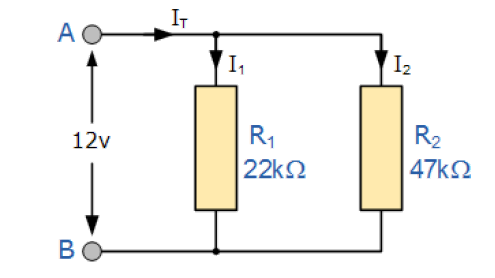
با استفاده از فرمول بالا برای دو مقاومت موازی، می‌توانیم مقاومت مجموع مدار را محاسبه کنیم:

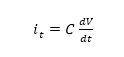
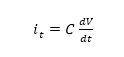
یک نکته مهم برای به خاطر سپردن درباره مقاومت های موازی این است که مقاومت مجموع مدار (R_T) هر دو مقاومت متصل به یکدیگر بصورت موازی همیشه کمتر از مقدار کوچکترین مقاومت در آن ترکیب خواهد بود.

در مقال فوق ما، مقدار ترکیب محاسبه شده بصورت R_T=15 بود بطوریکه، مقدار کوچکترین مقاومت 22 است که بالاتر است. در بیان دیگر، مقاومت معادل شبکه موازی همیشه کمتر از مقاومت مستقل کوچکتر در ترکیب خواهد بود.

همچنین، در حالتی که R1 معادل با R2 است R1=R2، مقاومت کلی شبکه همیشه نصف مقدار یکی از مقاومت‌ها R/2 خواهد شد.

به همین ترتیب، اگر سه با مقاومت بیشتر با مقدار یکسان بصورت موازی وصل شده باشند، سپس مقاومت مجموع معادل با R/n خواهد شد، بطوریکه Rمقدار مقاومت است و n تعداد مقاومت‌های مستقل در ترکیب است.

برای مثال، شش تا مقاومت 100 اهمی به یکدیگر در ترکیب موازی وصل شده اند. این مقاومت معادل در نتیجه بصورت R_T=R/n=100/6=16.7 Ω خواهد شد. اما توجه داشته باشید که این تنها برای مقاومت‌های معادل عملی است. این مقاومت‌ها همه مقدار یکسانی دارند.

جریان در مدار مقاومت های موازی

جریان کلی، I_T که به مدار مقاومتی موازی وارد می‌شود مجموع تمام جریان‌های مستقل که در تمام شاخه‌ها جاری می‌شود است. اما مقدار جریان جاری در هر شاخه موازی ممکن است ضرورتا یکسان نباشد زیرا که مقدار مقاومتی هر شاخه مقدار جریان جاری در آن شاخه را تعیین می‌کند.

برای مثال، اگرچه ترکیب موازی دارای ولتاژ یکسان در دو سر خود است، اما مقاومت‌ها می‌تواند متفاوت باشد در نتیجه جریان جاری در هر مقاومت می‌تواند قطعا متفاوت از مقداری که با قانون اهم اندازه‌گیری شده باشد.

دو مقاومت موازی فوق را در نظر بگیرید. جریانی که در هر مقاومت متصل بصورت موازی جاری می‌شود (I_R1 ,I_R2) ضرورتا مقدار یکسانی ندارند زیرا که آن بر مقدار مقاومتی مقاومت بستگی دارد. اگرچه، می‌دانیم که جریانی که به مدار از نقطه A وارد می‌شود باید در نقطه B مدار خارج شود.

قانون جریان کیرسهف بیان می‌کند که: “جریان کلی که مدار را ترک می‌کند معادل با آن است که وارد مدار می‌شود- جریانی گم نمی‌شود”. در نتیجه، جریان کلی جاری در مدار بصورت زیر است:

سپس با استفاده از قانون اهم، جریان جاری در هر مقاومت مثال شماره 2 در بالا می‌تواند بصورت زیر محاسبه شود:

جریان جاری در مقاومت R1

جریان جاری در مقاومت R2

درنتیجه جریان کلی مدار I_T در مدار بصورت زیر بدست می‌آید:

و این نیز می‌تواند مستقیما با استفاده از قانون اهم تایید شود:

رابطه داده شده برای محاسبه جریان مجموع جاری در مدار مقاومت های موازی که مجموع تمام جریان‌های مستقل اضافه شده به یکدیگر است، بصورت زیر است:

بنابراین شبکه‌ مقاومت های موازی نیز می‌توانند به عنوان “تقسیم‌کننده جریان” تصور شوند زیرا جریان تغذیه بین شاخه‌های مختلف موازی پخش یا تقسیم می‌شود. بنابراین یک مدار مقاومت موازی با داشتن N شبکه‌های مقاومتی، در حالی که دارای یک ولتاژ مشترک در دو سر خود است، دارای N مسیر جریان متفاوت با خواهد بود. مقاومت های موازی همچنین می‌توانند بدون تغییر مقاومت کل یا جریان کل مدار با یکدیگر تعویض شوند.

مثال شماره 3 مقاومت موازی

جریان‌های شاخه جداگانه و جریان کلی کشیده شده از منبع تغذیه را برای مجموعه مقاومت‌های زیر متصل به هم در یک ترکیب موازی محاسبه کنید.

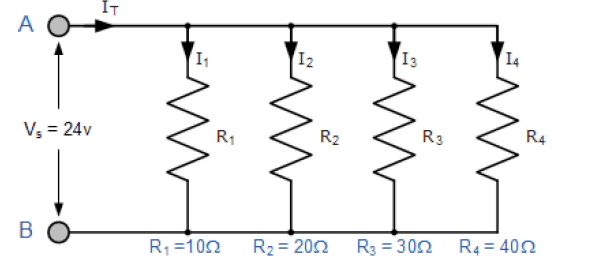
از آنجا که ولتاژ تغذیه برای همه مقاومت‌های موجود در مدار موازی مشترک است، می‌توانیم از قانون اهم برای محاسبه جریان شاخه جداگانه به شرح زیر استفاده کنیم.

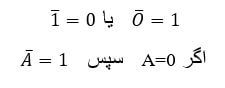
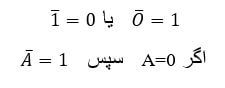
سپس جریان کلی مدار I_T جاری در ترکیب مقاومت های موازی بصورت زیر خواهد بود:

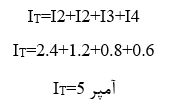
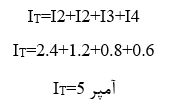
این مقدار جریان کلی مدار 5 آمپر را نیز می‌توان با یافتن مقاومت مدار معادل، R_T شاخه موازی و تقسیم آن به ولتاژ منبع تغذیه، Vs به شرح زیر یافت و تأیید کرد.

مقاومت معادل مدار:

سپس جریان جاری در مدار جاری خواهد شد.

خلاصه مقاومت های موازی

بنابراین به طور خلاصه، هنگامی که دو یا چند مقاومت به هم وصل می‌شوند به طوری که هر دو پایانه آنها به ترتیب به هر ترمینال مقاومت یا مقاومت دیگر متصل می‌شوند، گفته می‌شود که آنها به طور موازی به یکدیگر وصل می‌شوند. ولتاژ موجود در هر مقاومت در یک ترکیب موازی دقیقاً یکسان است، اما جریان‌هایی که از طریق آنها جریان می‌یابد یکسان نیستند زیرا این با مقدار مقاومت آنها و قانون اهم تعیین می‌شود. سپس مدارهای موازی تقسیم‌کننده جریان هستند.

مقاومت معادل یا کل، R_T یک ترکیب موازی از طریق افزودن کسر یافته می‌شود و مقدار مقاومت کل همیشه کمتر از کوچکترین مقاومت مستقل در ترکیب خواهد بود. شبکه‌های مقاومت موازی را می‌توان در همان ترکیب بدون تغییر مقاومت کل یا جریان کل مدار، در همان ترکیب قرار داد. مقاومت‌های متصل به هم در یک مدار موازی حتی اگر یک مقاومت مدار باز باشد به کار خود ادامه می‌دهند.

تا کنون دیدیم که شبکه‌های مقاومتی در دو حالت سری و موازی وصل می‌شوند. در آموزش بعدی درباره مقاومت‌ها، بر اتصال مقاومت‌ها در دو ترکیب سری و موازی در یک زمان که یک مدار مقاومت ترکیبی تولید می‌کند، خواهیم پرداخت.