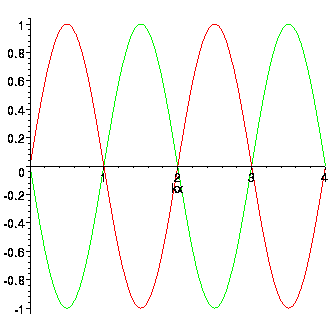
اختلاف فاز برای توصیف اختلاف در درجه یا رادیان هنگامی که دو یا چند کمیت متناوب به مقادیر بیشینه یا صفر میرسد به کار میبرد.
فهرست مطالب
اختلاف فار چیست
قبلا دیدیم که یک شکل موج سینوسی یک کمیت متغیر است که میتواند به صورت گرافیکی در حوزه زمان همراه با محور صفر افقی نمایش داده شود. همچنین دیدیم که به عنوان یک کمیت متغیر، موجهای سینوسی دارای یک مقدار بیشینه مثبت در زمان π/2، یک مقدار بیشینه منفی در زمان 3π/2 با مقادیر صفر است که در راستای خط پایه در 0، π ،2π است.
اگرچه، تمام شکل موجهای سینوسی به صورت دقیق از نقطه صفر محور در همان زمان نخواهد گذشت، اما ممکن است به راست یا چپ صفر درجه توسط برخی مقدار هنگامی که با یک موج سینوسی مقایسه میشود، “شیفت” یابد.
برای مثال، مقایسه یک شکل موج ولتاژ با یک شکل موج جریان است. این سپس یک شیفت زاویهای یا اختلاف فاز بین دو شکل موج سینوسی تولید میکند. هر موج سینوسی که از صفر در t=0 عبور نمیکند دارای یک شیفت فاز است.
شیفت فاز
اختلاف فاز یا شیفت فاز زاویه Φ (اصطلاح یونانی فی) در درجه یا رادیان یک شکل موج سینوسی نامیده میشود است که شکل موج از یک نقطه مرجع مشخص هم راستا با محور صفر افقی شیفت یافته است. در بیان دیگر، شیفت فاز اختلاف عرضی بین دو یا شکل موجهای بیشتر همراستا یک محور مشترک و شکل موجهای سینوسی همان فرکانس است که میتوان یک اختلاف فاز داشته باشد.
اختلاف فاز یک شکل موج متناوب میتواند از بین 0 تا پریود زمانی بیشینه خود شکل موج T در طول یک سیکل کامل تغییر کند و این میتواند هر جایی در راستای محور افقی بین Φ = 0 به 2π (رادیان) یا Φ = 0 تا 360 درجه بر طبق واحدهای زاویهای به کار رفته باشد.
اختلاف فاز همچنین میتواند به صورت یک شیفت زمانی T در ثانیه بیان شود و یک کسر پریود زمانی T را نشان میدهد برای مثال، +10ms یا -50µs اما به طور کلی بیان اختلاف فاز به صورت یک اندازه زاویهای بسیار رایج است.
سپس رابطه برای مقدار لحظهای یک ولتاژ سینوسی یا شکل موج جریان که در شکل موج سینوسی قبلی گسترش دادیم برای در نظر گرفتن زاویه فاز شکل موج، نیاز به اصلاح خواهد داشت و این بیان عمومی جدید به صورت زیر است:
رابطه اختلاف فاز
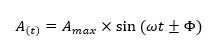
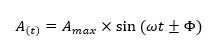
به طوریکه:


Φ (فی)- زاویه فاز در درجه یا رادیان است که شکل موج به چپ یا راست از نقطه مرجع شیفت یافته است. اگر شیب مثبت شکل موج سینوسی از محور افقی “قبل” t=0 عبور کند سپس شکل موج به چپ شیفت یافته است بنابراین Φ >0، و زاویه فاز در ذات خود مثبت +Φ خواهد شد و یک زاویه فاز پیش رو ارائه میکند. در بیان دیگر آن در زمان نسبت به 0 درجه زودتر ظاهر میشود و یک چرخش محور پاد ساعتگرد تولید میکند.
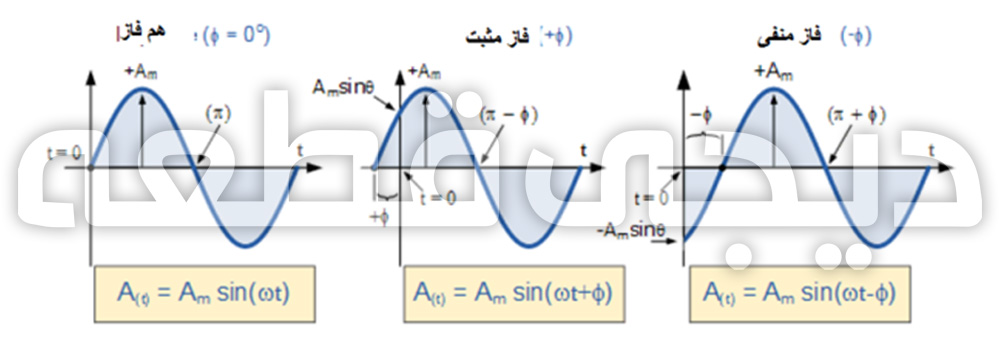
به همین ترتیب، اگر شیب مثبت شکل موج سینوسی از محور x افقی عبور کند در زمانی بعد از t=0، سپس شکل موج به راست شیفت مییابد بنابراین Φ <0، و زاویه فاز در ذات خود منفی -Φ خواهد شد و یک زاویه فاز تاخیری تولید میکند که آن در زمان نسبت به 0 درجه دیرتر ظاهر میشود و یک چرخش بردار ساعتگرد تولید میکند. هر دو حالت در زیر نشان داده شده است.
رابطه فاز یک شکل موج سینوسی

در ابتدا، بیایید دو کمیت متناوب مانند یک ولتاژ v و جریان i را در نظر بگیریم که دارای یک فرکانس مشترک f در هرتز هستند. از آنجا که فرکانس دو کمیت یکسان است سرعت زاویهای ω باید نیز یکسان باشد. بنابراین در هر لحظه در زمان میتوان گفت که فاز ولتاژ V همانند فاز جریان i خواهد بود.
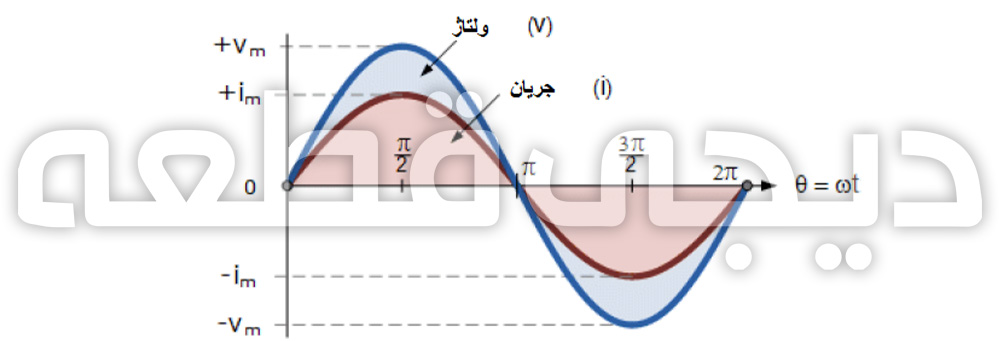
سپس زاویه چرخش درون یک پریود زمانی خاص همیشه یکی خواهد بود و اختلاف فاز بین دو کمیت v و i در نتیجه صفر و Φ = 0 خواهد بود. با یکسان بودن فرکانس ولتاژ V و جریان i، آنها باید هر دو به مقدار مثبت، منفی و صفر خود در طول یک سیکل کامل در همان زمان برسند (اگرچه دامنه آنها ممکن است متفاوت باشد). سپس گفته میشود که دو کمیت متناوب v و i “هم فاز” هستند.
دو شکل موج سینوسی “هم فاز”

اکنون بیایید فرض کنیم که ولتاژ V و جریان i دارای اختلاف فاز 30 درجه بین خود هستند بنابراین (Φ = 300 یا π/6 رادیان). با چرخش هر دو کمیت متناوب در یک سرعت یکسان، آنها فرکانس یکسان دارند، این اختلاف فاز برای تمام لحظات در زمان ثابت خواهد ماند، سپس اختلاف فاز 30 درجه بین دو کمیت توسط فی Φ نشان داده شده است که در زیر نیز نشان داده شده است.
اختلاف فاز یک شکل موج سینوسی
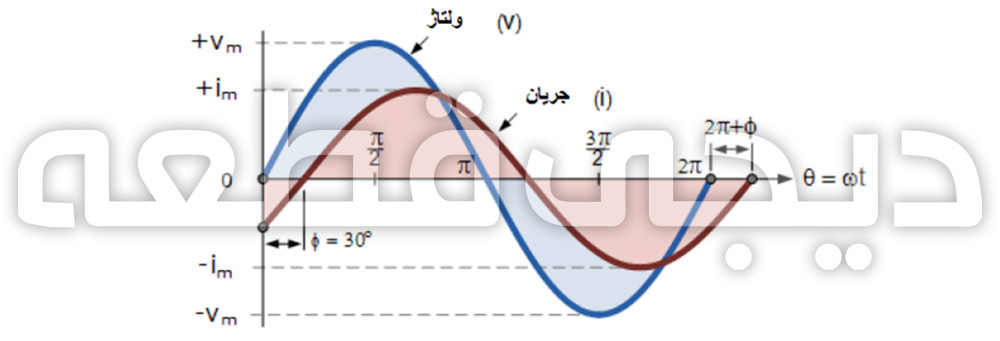

شکل موج جریان همچنان در مقدار، منفی است و این محور مرجع را تا بعد 30 درجه قطع نمیکند. سپس یک اختلاف فاز بین دو شکل موج وجود دارد و با قطع کردن محور مرجع افقی توسط جریان به اوج بیشینه خود و مقادیر صفر بعد از شکل موج ولتاژ میرسد.
از آنجا که دو شکل موج دیگر “هم فاز” نیستند، درنتیجه آنها باید توسط یک مقدار تعیین شده توسط فی Φ “غیر هم فاز” باشند و این فی در مثال ما 300 است. بنابراین میتوان گفت که دو شکل موج اکنون با 30 درجه با یکیدیگر اختلاف فاز دارند. همچنین میتوان گفت که شکل موج جریان نسبت به شکل موج ولتاژ با زاویه فاز Φ تاخیر دارد. سپس در مثال ما در بالا دو شکل موج دارای یک اختلاف فاز تاخیری هستند بنابراین عبارت برای هر دو ولتاژ و جریان بالا به صورت زیر خواهد بود:
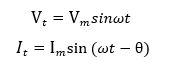
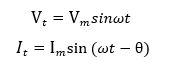
به طوریکه I با زاویه Φ نسبت به V تاخیر دارد.
به همین ترتیب اگر جریان i دارای یک مقدار مثبت باشد و محور مرجع را قطع کند به مقادیر اوج مثبت و صفر خود در بعضی زمان ها قبل از ولتاژ v میرسد و سپس شکل موج جریان نسبت به ولتاژ با زاویه فاز “پیش رو” خواهد بود. سپس گفته میشود که دو شکل موج دارای یک اختلاف فاز پیش رو هستند و عبارت برای هر دو ولتاژ و جریان به صورت زیر خواهد بود:
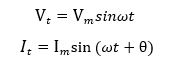
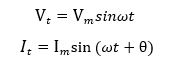
زاویه فاز یک موج سینوسی میتواند برای توصیف رابطه بین یک موج سینوسی با دیگری با استفاده از اصطلاح “پیش رو” و “تاخیر” برای نمایش رابطه بین دو شکل موج سینوسی هم فرکانس که در محورهای مرجع یکسان رسم شدهاند، به کار رود.
در مثال ما در بالا دو شکل موج با 30 درجه نسبت به یکدیگر غیر هم فاز هستند. بنابراین میتوان به صورت صحیح گفت که i دارای تاخیر نسبت به v است یا میتوان گفت که v نسبت به I طبق اینکه کدام یک به عنوان مرجع ما انتخاب شده، با 30 درجه پیش رو است.
رابطه بین دو شکل موج و زاویه فاز حاصل میتواند هرجایی هم راستا با محور صفر افقی از طریق اینکه کدام شکل موج با جهت”شیب یکسان” مثبت یا منفی میگذرد اندازهگیری شود. در مدارهای توان AC این توانایی برای توصیف رابطه بین یک ولتاژ و یک جریان موج سینوسی درون همان مدار بسیار مهم است و آنالیز پایه مدار AC را تشکیل میدهد.
شکل موج کوسینوسی
بنابراین اکنون میدانیم که هنگامی که یک شکل موج با موج سینوسی دیگر مقایسه میشود اگر به راست یا چپ 0 درجه “شیفت” یابد عبارت برای این شکل موج به صورت میشود. اما اگر شکل موج با یک شیب به سمت مثبت 90 درجه یا π/2 رادیان قبل از شکل موج مرجع، محور صفر افقی را قطع کند، شکل موج یک شکل موج سینوسی نامیده میشود و رابطه به صورت زیر است:
رابطه کوسینوسی
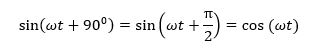
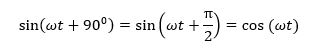
موج cosine که به سادگی “cos” نامیده میشود به اندازه موج سینوسی در مهندسی برق اهمیت دارد. موج کوسینوسی دارای همان شکل است که موج سینوسی با آن سر و کار دارد که آن یک تابع سینوسی است اما به صورت 90+ درجه یا یک ربع کامل یک پریود از آن شیفت یافته است.
اختلاف فاز بین یک موج سینوسی و یک موج کوسینوسی
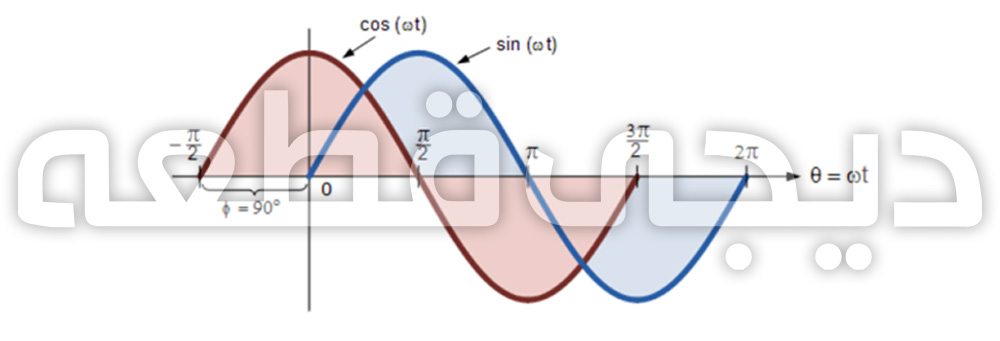

متناوبا، می توان گفت که یک موج سینوسی نیز یک موج کوسینوسی با شیفت 90 درجه است. همچنین هنگامی که با موجهای سینوسی یا کوسینوسی یک زاویه سر کار داریم، قوانین پیش رو همیشه اعمال خواهند شد.
روابط موج سینوسی و کوسینوسی
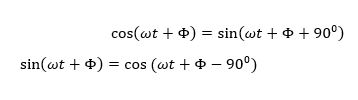
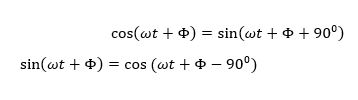
هنگامی که دو شکل موج سینوسی را مقایسه میکنیم بیان عبارت آنها به صورت یک سینوس یا کوسینوس با دامنههای به سمت مثبت بسیار رایج است و این با استفاده از روابط ریاضی زیر قابل دستیابی است:
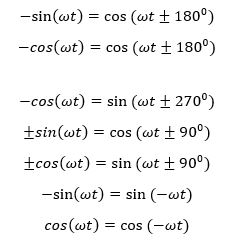
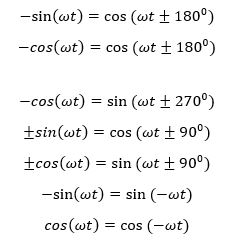
با استفاده از این روابط بالا میتوان هر شکل موج سینوسی با یا بدون یک اختلاف فاز یا زاویهای را از موج سینوسی به یک موج کوسینوسی یا بر عکس تبدیل کرد.
در آموزش بعدی درباره فازورها از یک متد گرافیکی نمایش یا مقایسه اختلاف فاز بین دو سینوسها با پرداختن بر نمایش فازوری یک فاز واحد کمیت AC هم راستا با برخی جبر فازور مربوط به جمع ریاضی دویا چند فازور استفاده خواهیم کرد.