زمانی که مقاومتها به صورت یک زنجیره در یک خط واحد به یکدیگر وصل شوند گفته میشود که آنها به صورت مقاومتهای سری با یکدیگر هستند که این منجر به یک شارش جریان مشترک در آنها میشود. مقاومتهای مستقل میتوانند هم به صورت اتصال سری و هم موازی یا ترکیبی از هردو سری و موازی برای تولید شبکههای مقاومتی پیچیده تر که مقاومت معادل آنها بصورت ترکیب ریاضی مقاومتهای مستقل متصل به یکدیگر است، میباشد.
فهرست مطالب
مقاومت سری
مقاومت تنها، یک مولفه الکترونیکی بنیادی که میتواند برای تبدیل یک ولتاژ به یک جریان یا یک جریان به ولتاژ استفاده شود نیست، اما با تنظیم صحیح مقدار آن، یک وزندهی متفاوت میتواند بر جریان و یا ولتاژ تبدیل شده قرار گیرد، که به آن اجازه استفاده در مدارهای مرجع ولتاژ و کاربردیها را میدهد.
مقاومتهای سری یا شبکههای مقاومتی پیچیده میتواند با یک مقاومت معادل واحد REQ یا امپدانس ZEQ جایگزین شود و ترکیب یا پیچیدگی شبکه مقاومت مهم نیست، تمام مقاومتها از قوانین پایه یکسان پیروی میکنند که به صورت قانون اهم و قوانین مدار کیریشهف تعریف شده، پیروی میکنند.
شکل گیری مدار سری مقاومتی
زمانی که مقاومتها به صورت یک زنجیره در یک خط واحد به یکدیگر وصل شده اند، گفته میشود که مقاومتها به صورت سری با یکدیگر هستند. از آنجا که تمام جریان شارشی در اولین مقاومت هیچ جایی برای شارش ندارد، آن باید از دومین و سومین مقاومت هم عبور کند و به همین ترتیب ادامه یابد. بنابراین، مقاومتهای سری، دارای یک شارش جریان مشترک از خود هستند به طوریکه جریانی که از یک مقاومت عبور میکند باید از بقیه مقاومتها نیز عبور کند زیرا که آن تنها یک مسیر دارد. سپس مقدار جریان شارشی در مجموعهای از مقاومتهای سری در تمام نقاط شبکه مقاومت سری یکسان خواهد بود. برای مثال:
[latexpage]
[
I_{R1}=I_{R2}=I_{R3}=I_{AB}=1MA
]
در مثال پیش رو مقاومتهای R1 ,R2 و R3 همگی با هم بصورت سری بین نقطه A و B با یک جریان مشترک I که از آنها شارش مییابد، وصل شدهاند.
مدار مقاومتی سری


از آنجا که مقاومت ها به صورت سری با یکدیگر هستند جریان یکسان از هر مقاومت در زنجیره عبور میکند و مقاومت مجموع RT مدار باید برابر با جمع تمام مقاومتهای مستقل که به یکدیگر اضافه شدهاند، باشد. که به صورت:
[latexpage]
[
R_T=R_1+R_2+R_3
]
درنتیجه با قرار دادن مقادیر مقاومتها در مثال ساده فوق، مقاومت معادل کلی REQ بصورت زیر ارائه میشود:
[latexpage]
[
R_{EQ}=R_1+R_2+R_3=1KOmega+2KOmega+6KOmega=9KOmega
]
بنابراین دیدیم که میتوان 3 مقاومت مستقل را با تنها یک مقاومت “معادل” واحد جایگزین کرد که دارای مقدار 9kΩ است. به طوری که 4، 5 یا حتی مقاومتهای بیشتر که همگی باهم در یک مدار سری متصل شده اند، مقاومت معادل یا مجموع مدار RT همچنان مجموع تمام مقاومتهای مستقل متصل به یکدیگر خواهد بود و هر چه مقاومت بیشتری به مجموعه اضافه شود مقاومت مجموع بیشتر میشود (مقادیر آنها اهمیت ندارد).
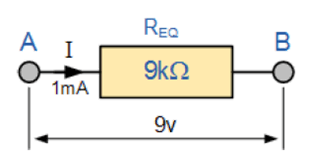
مقاومت کلی عموما به صورت مقاومت معادل شناخته میشود و میتواند به صورت ؛ “یک مقدار واحد از مقاومت که میتواند با هر مقاومت سری بدون تغییر مقدار ولتاژ و جریان در مدار جایگزین شود” است. سپس رابطه برای محاسبه مقاومت مجموع مدار هنگامی که مقاومتها به صورت سری با یکدیگر وصل شدهاند به صورت زیر ارائه شده است:
فرمول مقاومت سری
[latexpage]
[
R_total=R_1+R_2+R_3+…+R_n
]
توجه داشته باشید که مقاومت مجموع یا معادل RT دارای همان تاثیر ترکیب اصلی مقاومتها بر روی مدار است به طوری که آن جمع جبری مقاومتهای مستقل است. اگر دو مقاومت یا امپدانس سری با یکدیگر برابر باشند و مقدار یکسانی داشته باشند، سپس مقاومت معادل یا مجموع RT معادل با دو برابر مقدار یک مقاومت است. این برابر با 2R و برای سه مقاومت برابر سری 3R و غیره خواهد بود .
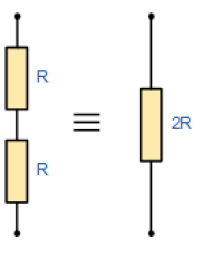

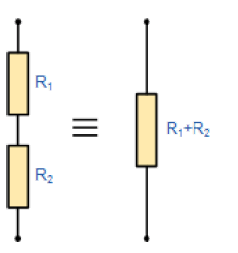

اگر دو مقاومت یا امپدانس سری نابرابر باشند و مقادیر متفاوت داشته باشند، سپس مقاومت مجموع یا معادل RT برابر با جمع ریاضی دو مقاومت، برابر با R1+R2 است. اگر 3 یا مقاومت نابرابر بیشتری (یا برابر) به صورت سری به یکدیگر وصل باشند سپس مقاومت معادل برابر است با:
[latexpage]
[
R_1+R_2+R_3+…
]
یک نکته مهم که در مورد مقاومتها در شبکههای سری باید به خاطر سپرد، بررسی درست بودن ریاضیات است. مقاومت مجموع (RT) هر دو یا مقاومت بیشتر متصل به یکدیگر به صورت سری همیشه بزرگتر از بزرگترین مقدار مقاومت در زنجیره خواهد بود. در مثال فوق RT=9kΩ به طوری که بزرگترین مقاومت دارای مقدار 6kΩ است.
ولتاژ مقاومت سری
ولتاژ دو سر هر مقاومت وصل شده به صورت سری از قوانین متفاوت از جریان پیروی میکند. از مدار فوق میدانیم که ولتاژ تغذیه کلی دو سر مقاومتها برابر با مجموع اختلاف پتانسیل دو سر R1 ,R2 و R3 به صورت میباشد:
[latexpage]
[
V_{AB}=V_{R1}+V_{R2}+V_{R3}=9V
]
با به کار بردن قانون اهم، ولتاژ دو سر مقاومتهای مستقل میتواند به صورت زیر محاسبه شود:
[latexpage]
[
R_1=I_{R1}=1mA*1KOmega=1V
]
[latexpage]
[
R_2=I_{R2}=1mA*2KOmega=2V
]
[latexpage]
[
R_3=I_{R3}=1mA*6KOmega=6V
]
که ولتاژ مجموع VAB=(1V+2V+6V)=9V خواهد شد که برابر با مقدار ولتاژ تغذیه است. سپس مجموع اختلاف پتانسیل دو سر مقاومتها برابر با اختلاف پتانسیل دو سر ترکیب میباشد و در مثال ما این برابر 9 ولت است. رابطه ارائه شده برای محاسبه ولتاژ مجموع در یک مدار سری که جمع تمام ولتاژهای مستقل اضافه شده به یکدیگر است به صورت زیر میباشد:
[latexpage]
[
V_{total}=V_{R1}+V_{R2}+V_{R3}+…+V_N
]
سپس شبکههای مقاومت سری نیز میتواند به صورت “تقسیم کنندههای ولتاژ” در نظر گرفته شوند، و یک مدار مقاومت سری دارای N مولفه مقاومتی، N ولتاژ مختلف دو سر آن خواهد داشت در حالی که یک جریان مشترک را حفظ میکنند. با استفاده از قانون اهم، ولتاژ، جریان یا مقاومت هر مدار متصل سری میتواند به راحتی پیدا شود و مقاومت یک مدار سری میتواند بدون تحت تاثیر قرار دادن مقاومت مجموع، جریان یا توان به هر مقاومت تغییر یابد.
مثال شماره 1 مقاومتهای سری
با استفاده از قانون اهم، مقاومت سری معادل، جریان سری، افت ولتاژ و توان را برای هر مقاومت در مدار سری پیش رو را محاسبه کنید.
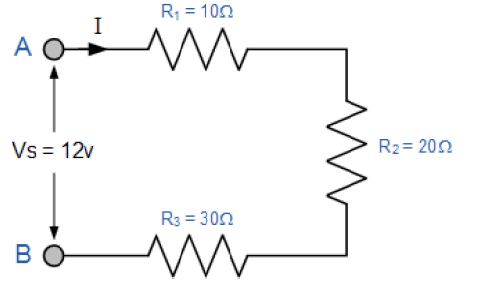
تمام اطلاعات میتواند با استفاده از قانون اهم به دست آید، و برای آسانتر کردن روند میتوان این اطلاعات را در شکل جدولی نشان داد.
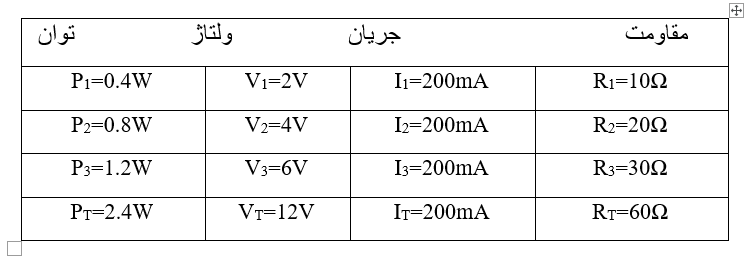

سپس برای مدار فوق، RT=60 Ω، IT=200mA، VT=12V، PT=2.4W است.
مدار تقسیم کننده ولتاژ
از مثال فوق میتوان دید که، اگرچه ولتاژ تغذیه به صورت 12 ولت است، اما ولتاژهای مختلف یا افت ولتاژ در دوسر هر مقاومت در داخل شبکه سری ظاهر میشود. وصل کردن مقاومتها به صورت سری بر دو سر یک منبع تغذیه DC دارای یک مزیت اصلی است، ولتاژهای مختلف ظاهر شده بر دو سر هر مقاومت یک مدار بسیار دستی که یک شبکه تقسیمکننده ولتاژ نامیده میشود، به وجود میآورد.
این مدار ساده، ولتاژ تغذیه را متناسبا در دو سر هر مقاومت سری در زنجیره با مقدار افت ولتاژ تعیین شده توسط مقدار مقاومتها تقسیم میکند و همانطور که میدانیم جریان عبوری از یک مدار مقاومت سری برای تمام مقاومتها مشترک است. بنابراین مقاومت بزرگتر دارای یک افت ولتاژ بزرگتر در دو سر خود خواهد بود، درحالی که مقاومت کوچکتر افت ولتاژ کوچکتری در دوسر خود خواهد داشت.
مدار مقاومتی سری نشان داده شده در بالا یک شبکه تقسیمکننده ولتاژ ساده را تشکیل میدهد به طوریکه سه ولتاژ 2 ولت، 4 ولت و 6 ولت از یک منبع تغذیه 12 ولت واحد تولید شدهاند. قانون ولتاژ کیریشهف بیان میکند که “ولتاژ تغذیه در یک مدار بسته برابر با مجموع تمام افت ولتاژهای (I×R) در اطراف مدار است” و این برای اثر بخشی خوب میتواند به کار رود.
قانو تقسیم ولتاژ، به ما اجازه میدهد تا از تاثیرات مقاومت متناسبا برای محاسبه اختلاف پتانسیل دو سر هر مقاومت بدون توجه به جریان جاری در مدار سری استفاده کنیم. یک “مدار تقسیم کننده ولتاژ” نوعی در زیر نشان داده شده است.
شبکه تقسیم کننده ولتاژ
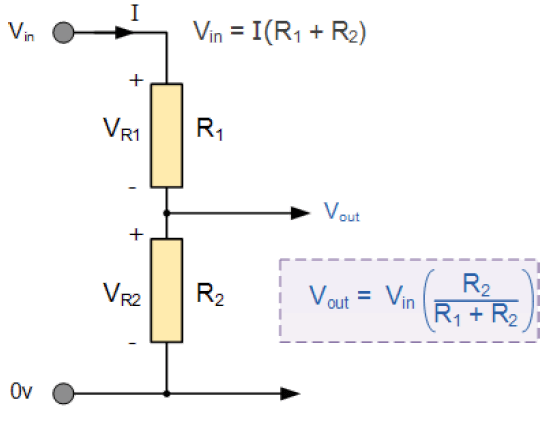

مدار نشان داده شده، متشکل از تنها دو مقاومت R1 و R2 متصل به یکدیگر به صورت سری در دوسر ولتاژ تغذیه Vin است. یک بخش از ولتاژ تغذیه توان به مقاومت R1 وصل شده و خروجی ولتاژ Vout از دو سر مقاومت R2 گرفته میشود. مقدار این ولتاژ خروجی توسط فرمول متناظر ارائه شده است.
اگر مقاومتهای بیشتری به صورت سری به مدار وصل شوند سپس ولتاژهای مختلفی در دو سر هر مقاومت به نوبت با توجه به مقدار مقاومت مستقل R خود (قانون اهم I×R) ظاهر خواهد شد که نقاط ولتاژ متفاوت اما کوچکتر از یک تغذیه واحد را مهیا خواهند کرد. بنابراین اگر ما سه یا مقاومت های بیشتری را در زنجیره سری داشتیم، ما همچنان میتوانیم فرمول تقسیمکننده پتانسیل آشنای خود را برای یافتن افت ولتاژ دو سر هر کدام به کار ببریم. مدار زیر را در نظر بگیرید.
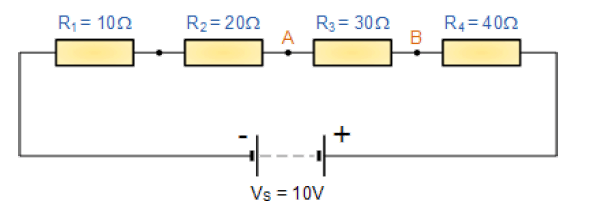

مدار تقسیمکننده ولتاژ فوق، چهار مقاومت متصل به یکدیگر سری را نشان میدهد. افت ولتاژ دو سر نقاط A و B با استفاده از فرمول تقسیمکننده پتانسیل به صورت زیر میتواند محاسبه شود:
[latexpage]
[
V_AB=V_R3=V_s×R_3/(R_1+R_2+R_3+R_4 )
]
[latexpage]
[
V_AB=10×30/(10+20+30+40)=10×0∙3=3V
]
ما همچنین میتوانیم همان ایده را برای یک گروه از مقاومتهای سری به کار ببریم. برای مثال اگر میخواستیم تا افت ولتاژ دو سر هر دو مقاومت R2 و R3 با هم را بیابیم، باید مقدار آنها را در فرمول شمارشی جایگذاری میکردیم و در این حالت جواب حاصل به ما 5 ولت (2V+3V) را خواهد داد.
در این مثال بسیار ساده ولتاژها بسیار منظم کار میکنند به طوری که افت ولتاژ دو سر یک مقاومت متناسب با مقاومت مجموع است، و از آنجا که مقاومت مجموع (RT) در این مثال برابر با 100 اهم یا 100% است، مقاومت R1 10% مقاومت RT است بنابراین 10% ولتاژ منبع VS در دوسر آن، 20% VS در دوسر مقاومت R2 ،30% دو سر مقاومت R3، و 40% ولتاژ تغذیه VS در دوسر مقاومت R4 ظاهر خواهد شد. به کار بردن قانون ولتاژ کیریشهف (KVL) در اطراف مسیر حلقه بسته این را اثبات میکند.
اکنون بیایید فرض کنیم که میخواهیم دو مدار تقسیم کننده ولتاژ مقاومت فوق را برای تولید یک ولتاژ کوچکتر از یک ولتاژ تغذیه بزرگتر برای توان و مدار الکترونیکی بیرونی به کار ببریم. فرض کنید یک تغذیه 12ولت DC داریم و مدار ما که دارای یک امپدانس 50 اهم است تنها نیازمند یک تغذیه 6 ولتی، نصف ولتاژ است.
وصل کردن دو مقاومت با مقدار برابر هر کدام 50 اهم با هم، به عنوان یک شبکه تقسیمکننده ولتاژ دو سر 12 ولت تا زمانی که ما مدار بار را به شبکه وصل کنیم، این را بسیار زیبا انجام خواهد داد. این بدان دلیل است که تاثیر بارگذاری مقاومت RL متصل به صورت موازی در دو سر R2 نسبت دو مقاومت سری و افت ولتاژ آنها را تغییر میدهد و این در زیر نشان داده شده است.
مثال شماره 2 مقاومتهای سری
افت ولتاژ های دو سر Xو Y را محاسبه کنید
الف) بدون اتصال RL
ب) با اتصال RL
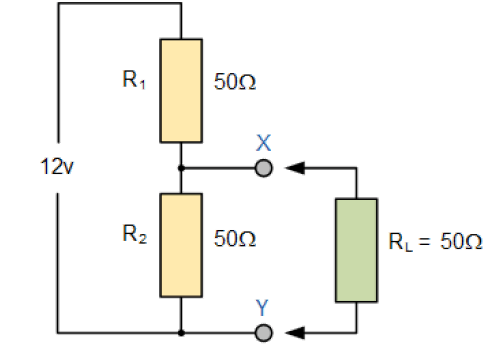

الف) بدون اتصال Rl
[latexpage]
[
R_{x-y}-50Omega
]
[latexpage]
[
V_out=V_in×R_2/(R_1+R_2 )
]
[latexpage]
[
V_out=12×50/(50+50)=6V
]
ب) با اتصال RL
[latexpage]
[
R_{x-y}=25Omega
]
[latexpage]
[
V_out=V_in×R_2/(R_1+R_2 )
]
[latexpage]
[
V_out=12V×25/(50+25)=4V
]
همانطور که میبینید، ولتاژ خروجی Vout بدون اتصال مقاومت بار به ما ولتاژ خروجی مورد نیاز 6 ولت را میدهد اما همان ولتاژخروجی در Vout هنگامی که بار وصل شده است به تنها 4 ولت افت میکند (مقاومتهای سری). سپس میتوان دید که یک شبکه تقسیمکننده ولتاژ، ولتاژ خروجی خود را به عنوان نتیجه تاثیر بارگذاری تغییر میدهد، زیرا که ولتاژ خروجی Vout توسط نسبت R1 به R2 تعیین شده است. اگرچه، با افزایش مقاومت بار RL تا بینهایت (∞) این تاثیر بار گذاری کاهش مییابد و نسبت ولتاژ Vout/VS با اضافه شدن بار در خروجی بدون تاثیر میماند. سپس هر چه امپدانس بار بیشتر باشد، تاثیر بارگذاری در خروجی کمتر میشود.
تاثیر کاهش یک سطح سیگنال یا ولتاژ به عنوان تضعیف شناخته میشود بنابراین هنگام استفاده از یک شبکه تقسیمکننده ولتاژ باید به این امر دقت شود. این تاثیر بارگذاری با استفاده از یک پتانسیومتر به جای مقاومتهای مقدار ثابت و تنظیم تطابقی میتواند جبران شود. این روش همچنین برای جبران تقسیمکننده پتانسیل برای تولرانسهای متغیر در ساختار مقاومتها نیز به کار میرود.
یک مقاومت متغیر، پتانسیومتر یا پات که بیشتر به این نام معروف است، یک مثال خوب برای یک تقسیمکننده ولتاژ چند مقاومتی درون یک بستهبندی واحد است زیرا که آن میتواند به صورت هزاران عدد مقاومت کوچک سری در نظر گرفته شود. اینجا یک ولتاژ ثابت در دو سر دو اتصال ثابت بیرونی اعمال شده است و ولتاژ خروجی متغیر از پایانه عقربه گرفته شده است. پتانسیومترهای چند چرخشی کنترل دقیقتر ولتاژ خروجی را ممکن میسازند.
مدار تقسیمکننده ولتاژ ساده ترین روش تولید یک ولتاژ پایین تر از یک ولتاژ بالاتر است و یک مکانیسم عملیاتی پایه پتانسیومتر است.
همانند استفاده برای محاسبه ولتاژ تغذیه پایین تر، فرمول تقسیمکننده ولتاژ همچنین میتواند در تحلیل مدارهای مقاومتی پیچیدهتر شامل هر دو شاخههای سری و موازی نیز به کار رود. فرمول تقسیمکننده پتانسیل یا ولتاژ میتواند برای تعیین افت ولتاژها اطراف یک شبکه DC بسته یا به عنوان بخشی ازقوانین تحلیل مدار گوناگون مانند کیریشهف یا قضیه تونین به کار رود.
کاربرد مقاومت سری
دیدیم که مقاومتهای سری میتوانند برای تولید ولتاژهای مختلف در دوسر خود به کار روند و این نوع از شبکه مقاومت برای تولید یک شبکه تقسیم کننده ولتاژ بسیار کاربردی است. اگر یکی از مقاومتها را در مدار تقسیمکننده ولتاژ فوق با یک سنسور مانند ترمیستور، مقاومت وابسته بر نور (LDR[1])یا حتی یک سوئیچ جایگزین کنیم، میتون یک کمیت آنالوگ سنجش شده را به یک سیگنال الکتریکی مناسب که قابل اندازهگیری است تبدیل کرد.
برای مثال، مدار ترمیستور پیش رو دارای یک مقاومت 10 کیلو اهم در 25 درجه سانتیگراد و یک مقاومت 100 اهم در 100 درجه سانتیگراد است. ولتاژ خروجی (Vout)برای هر دو دما را محاسبه کنید.
مدار ترمیستور
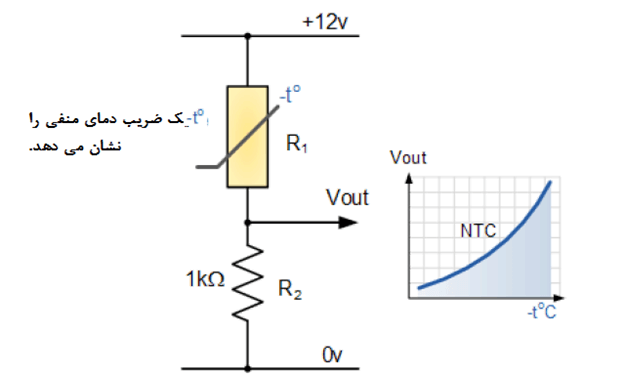
در دمای 25 درجه سانتیگراد:
[latexpage]
[
V_out=V_in×R_2/(R_1+R_2 )=12×1000/(10000+1000)=1∙09V
]
در دمای 100 درجه سانتیگراد:
[latexpage]
[
V_out=V_in×R_2/(R_1+R_2 )=12×1000/(100+1000)=10∙9V
]
بنابراین با تغییر مقاومت R2 1kΩ ثابت در مدار ساده فوق به یک مقاومت متغیر یا پتانسیومتر، نقطه تنظیم ولتاژ خروجی خاص در طول یک محدوده دمای عریضتر میتواند به دست آید.
خلاصه مقاومتهای سری
هنگامی که دو یا مقاومتهای بیشتری به یکدیگر به صورت انتها به انتها در یک شاخه واحد وصل شدند، گفته میشود که مقاومتها به صورت سری به یکدیگر وصل شدهاند. مقاومتهای سری جریان یکسانی را حمل میکنند اما افت ولتاژ دو سر آنها برابر با مقادیر مقاومتهای مستقل نیست هر مقاومت دارای افت ولتاژ متفاوت از دیگری خواهد بود که توسط قانون اهم (V=I×R) تعیین میشود. سپس مدارهای سری تقسیمکننده ولتاژ هستند.
در شبکه مقاومت سری مقاومتهای مستقل به یکدیگر برای یک مقاومت معادل (RT) از ترکیب سری اضافه میشوند. مقاومتها در مدار سری میتوانند بدون تحت تاثیر قرار دادن مقاومت مجموع، جریان یا توان به هر مقاومت یا مدار مبادله شوند.
در آموزش بعدی درباره مقاومتها، بر اتصال مقاومتها بصورت موازی خواهیم پرداخت و نشان میدهیم که مقاومت کلی عکس جمع تمام مقاومت اضافه شده به یکدیگر است و ولتاژ برای یک مدار موازی مشترک است. همچنین برای خرید مقاومت میتوانید به فروشگاه سایت دیجی قطعه مراجعه کنید.



