تبدیل اعداد دودویی به ده دهی 

تبدیل اعداد دودویی به ده دهی از ستون‌های وزن‌دار برای تشخیص مرتبه ارقام برای تعیین مقدار نهایی عدد استفاده می‌کند.

تبدیل اعداد دودویی به ده دهی

تبدیل اعداد دودویی به ده دهی ( مبنا 2 به مبنا 10) و برعکس یک مفهوم مهم برای یادگیری است زیرا که سیستم اعداد دودویی پایه‌ای را برای تمام سیستم‌های کامپیوتری و دیجیتال تشکیل می‌دهد. سیستم شمارش ده دهی یا “ده دهی” از مبنای 10 سیستم شماره‌گذاری استفاده می‌کند به ‌طوریکه هر رقم در یک عدد یکی از ده مقدار ممکن از 0 تا 9 را بر می‌دارد که ” ارقام” نامیده می‌شود برای مثال 213₁₀ ( دویست و سیزده).

اما مانند داشتن 10 رقم ( 0 تا 9)، سیستم شماره‌گذاری ده دهی همچنین دارای عملگرهایی از جمع (+)، تفریق(-)، ضرب(×) و تقسیم(÷) است. در یک سیستم ده دهی هر رقم دارای یک مقدار 10 برابر بزرگتر از عدد قبلی خود است و این سیستم شماره‌گذاری اعشاری یک مجموعه‌ای از نمادها، b، با هم با یک مبنای q، را برای تعیین وزن هر رقم در داخل یک عدد استفاده می‌کند. برای مثال، شش در شصت دارای وزن کمتر از شش در ششصد است. سپس در یک سیستم شماره‌گذاری دودویی، نیازمند بعضی روش‌های تبدیل ده دهی به دودویی همانند برعکس از دودویی به ده دهی هستیم.

هر سیستم شماره‌گذاری می‌تواند توسط روابط زیر خلاصه شود:

N=b_i qⁱ

بطوریکه:

N یک عدد مثبت حقیقی است.

b رقم است.

q مقدار مبنا است.

و عدد صحیح (i) می‌تواند مثبت، منفی یا صفر باشد.

غیره……..N=b_n qⁿ….. b₃ q³+ b₂ q² + b₁ q¹ + b₀ q⁰ + b_-1 q^-1 + b_-2 q^-2

سیستم شماره گذاری ده دهی

در ده دهی، مبنای 10 (دهگان) یا سیستم شماره‌گذاری دهدهی، هر ستون عدد صحیح دارای مقدارهای واحد ده، صد، هزار و غیره هستند زیرا که در راستای عدد از راست به چپ حرکت می‌کنیم. بصورت ریاضی این مقادیر بصورت 10⁰, 10¹,10²,10³ و غیره هستند. سپس هر موقعیت به سمت چپ نقطه اعشار یک توان مثبت افزایشی از 10 را نشان می‌دهد. به همین طریق، برای اعداد معکوس، وزن عدد هنگامی که از چپ به راست می‌رویم، [latex] 10^{-3}, 10^{-2},10^{-1} [/latex] و غیره  منفی تر می‌شود. بنابراین، می‌توان دید که “سیستم شماره گذاری ده دهی” دارای مبنای 10 یا ماژول -10 (بعضی اوقات مد-10نامیده شده) با موقعت هر رقم در سیستم ده دهی که نشان‌دهنده اندازه یا وزن آن رقم به عنوان q برابر با “10” (0 تا9) است. برای مثال،  20( بیست) برابر با گفتن10¹× 2  است و درنتیجه 400 (چهارصد)  برابر با گفتن10²× 4  است.

مقدار هر عدد ده دهی برابر با مجموع ارقام ضرب در وزن های متناظر خودشان خواهند بود. برای مثال: N=6163₁₀ (شش هزار یکصد شصت و سه) در یک فرمت اعشار برابر است با:

6163 =6000+100+60+3

یا با وارد کردن وزن‌های هر رقم می‌توان بصورت زیر نوشت:

(6×1000)+ (1×100) + (6×10) + (3×1) =6163

یا آن می‌تواند در قالب مبنای ده بصورت زیر نوشته شود:

(6×10³)+ (1×10²) + (6×10¹) + (3×10⁰) =6163

بطوریکه در این مثال سیستم شماره‌گذاری ده دهی، چپ‌ترین رقم، مهمترین رقم یا MSD¹ است و راست‌ترین رقم کم اهمیت‌ترین رقم  یا LSD² است. در بیان دیگر، رقم 6 MSD است زیرا که موقعیت چپ‌ترین آن وزن بیشتری را حمل می‌کند و عدد 3  LSD است زیرا که موقعیت راست‌ترین آن کمترین وزن را حمل می‌کند.

سیستم شماره گذاری دودویی

در تبدیل اعداد دودویی به ده دهی، سیستم شماره‌گذاری دودویی، از بنیادی‌ترین سیستم شماره‌گذاری در تمام سیستم‌های مبتنی بر دیجیتال و کامپیوتر است و اعداد  دودویی از همان مجموعه قوانین سیستم شماره‌گذاری ده دهی پیروی می‌کنند. اما برخلاف سیستم ده دهی که از توان ده استفاده می‌کند، سیستم شماره‌گذاری دودویی بر روی توان دو کار می‌کند و یک تبدیل دودویی به ده دهی از مبنای2 به مبنای 10 ارائه می‌کند.

منطق دیجیتال و سیستم‌های کامپیوتری تنها دو مقدار یا حالت را برای نشان دادن یک شرط، یک سطح منطق “1” یا سطح منطق “0” به‌کار می‌برند و هر “0” و “1” به صورت یک  رقم واحد در مبنای 2 (دو) یا “سیستم شماره‌گذاری دودویی” در نظر گرفته می‌شود.

در سیستم شماره‌گذاری دودویی، یک عدد دودویی مانند 101100101 بصورت رشته‌ای از “1” ها و “0” ها با هر رقم در امتداد رشته از راست به چپ  با داشتن مقداری دو برابر مقدار قبلی  نشان داده می‌شود. اما از آنجا که این یک رقم دودویی است، تنها می‌تواند یک مقدار “1” یا “0” داشته باشد، بنابراین q برابر با “2” (0 یا 1) با موقعیت آن که نشان دهنده وزن آن در رشته است، می‌باشد.

از آنجا که عدد اعشار عدد وزن داده شده است، تبدیل از ده دهی به دودویی (مبنای 10 به مبنای 2) نیز یک عدد دودویی وزن‌دار با راست‌ترین بیت که کم اهمیت‌ترین بیت یا LSB و چپ‌ترین بیت که مهمترین بیت  یا MSB است را تولید خواهد کرد و می‌توان این را بصورت زیر نمایش داد:

نمایش یک عدد دودویی

در بالا دیدیم که در سیستم عدد ده دهی، وزن هر رقم از راست به چپ با ضریب 10 افزایش می‌یابد. در سیستم عدد دودویی، وزن هر رقم همانطور که نشان داده شده است با ضریب 2 افزایش می‌یابد. سپس رقم اول دارای یک وزن 1(2⁰)، رقم دوم دارای یک وزن 2(2¹)، سومین دارای وزن 4(2²)، چهارمین دارای وزن  8(2³) است و به همین ترتیب ادامه دارد. بنابراین برای مثال، تبدیل عدد دودویی به ده دهی به صورت زیر خواهد بود:

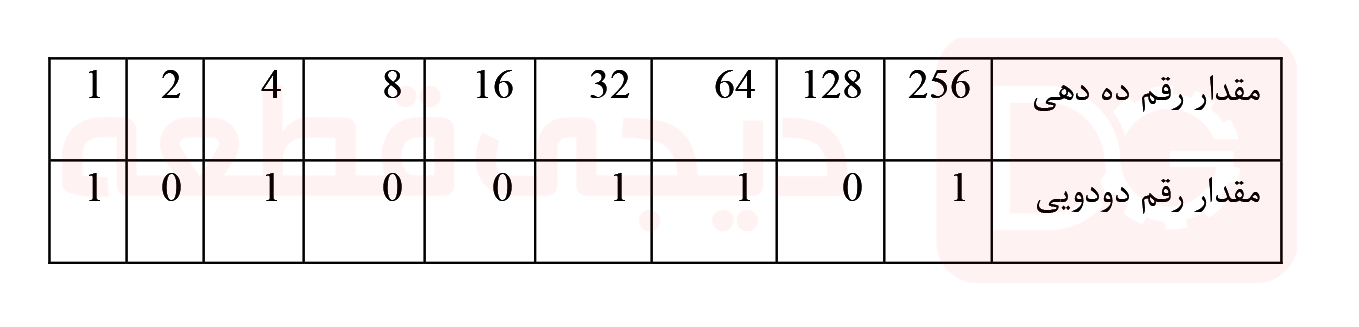
با اضافه کردن تمام مقدارهای عدد ده دهی از راست به چپ  با یکدیگر در موقعیت‌هایی که با “1” نشان داده شده‌اند به : (256)+(64)+(32)+(4)+(1)=357₁₀یا سیصد و پنجاه و هفت به عنوان یک عدد ده دهی دست می‌‌یابیم. سپس، می‌توان دودویی را به ده دهی با یافتن معادل ده دهی از آرایه دودویی ارقام 101100101₂  تبدیل کرد و می‌توان ارقام دودویی را در یک سری با مبنای 2 بسط داد که یک معادل 357₁₀  در اعشار یا ده دهی ارائه می‌کند. توجه داشته باشید که در سیستم تبدیل اعداد، “زیر نویس‌ها” برای نشان دادن سیستم شماره‌گذاری مبنای مربوطه، 9₁₀ = 1001₂ استفاده می‌شوند. اگر بعد از یک عدد از هیچ زیرنویسی استفاده نشود، معمولاً فرض می شود که عدد ده دهی است.

روش تقسیم بر 2 تکرار شده در تبدیل اعداد دودویی به ده دهی:

در بالا نحوه تبدیل اعداد دودویی به ده دهی را دیدیم، اما چگونه یک عدد ده دهی را به یک عدد دودویی تبدیل می‌کنیم. یک روش آسان برای تبدیل اعداد ده دهی به معادل‌های آن در دودویی، نوشتن عدد ده دهی و تقسیم مداوم بر 2 (دو) برای رسیدن به نتیجه و یک باقی مانده “1” یا “0” تا رسیدن به نتیجه نهایی معادل با صفر است. بنابراین به عنوان مثال. عدد ده دهی 294₁₀ را به عدد دودویی معادل تبدیل کنید.

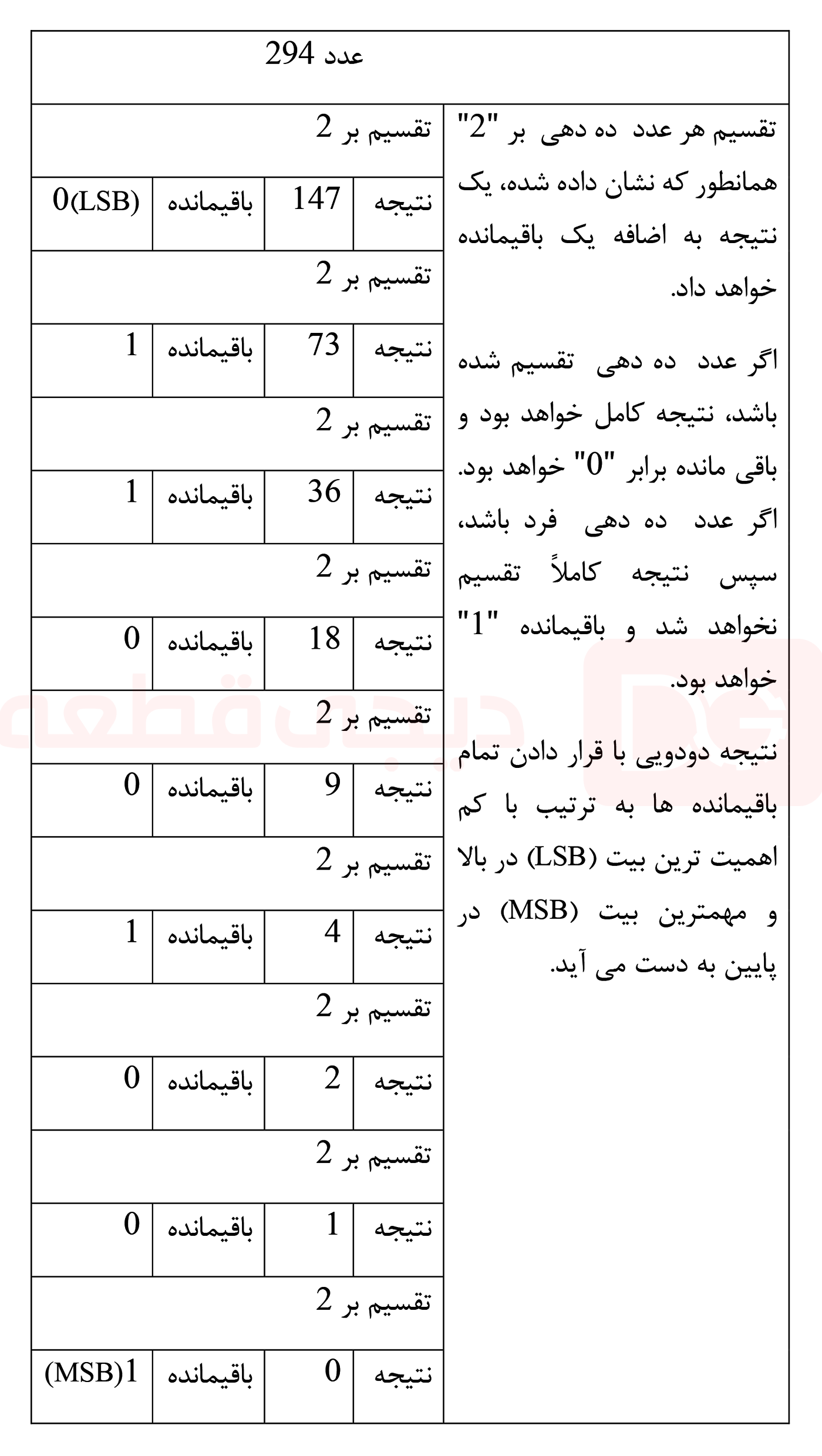
این تکنیک تقسیم بر 2 تبدیل عدد دودویی به ده دهی،  عدد ده دهی  294₁₀ معادل با 100100110₂ در دودویی خواندن از راست به چپ را ارائه می‌دهد. این روش تقسیم بر 2 برای تبدیل به سایر مبناهایی عددی نیز کار خواهد کرد.

سپس می‌توان دید که ویژگی‌های اصلی یک سیستم شماره‌گذاری دودویی این است که هر “رقم دودویی” یا “بیت” دارای یک مقدار “1” یا “0” است که هر بیت دارای وزن یا مقدار دو برابر از بیت قبلی خود است که از  کمترین یا کم اهمیت‌ترین بیت (LSB) شروع می شود و این روش “جمع وزنها” خوانده می‌شود. بنابراین می‌توان با استفاده از روش جمع وزن‌ها یا با استفاده از روش تکراری تقسیم بر دو نشان داده شده، یک عدد ده دهی را به یک عدد دودویی تبدیل کرد و با پیدا کردن مجموع وزن‌های آن، می‌توانیم عدد دودویی را به اعشار تبدیل کنیم.

اسامی عدد دودویی و پیشوندها

در تبدیل اعداد دودویی به ده دهی، اعداد دودویی مانند اعداد ده دهی می‌توانند با هم جمع و تفریق شوند و نتیجه آن بسته به تعداد بیت های مورد استفاده در یکی از محدوده های اندازه مختلف ترکیب می‌شوند. اعداد دودویی در سه حالت پایه ارائه می‌شوند – یک بیت، یک بایت و یک کلمه، که در آن بیت یک رقم دودویی واحد، یک بایت هشت رقم دودویی و یک کلمه 16 رقم دودویی است. طبقه بندی بیت های مستقل در گروههای بزرگتر عموماً با نامهای متداول زیر ذکر می شود:

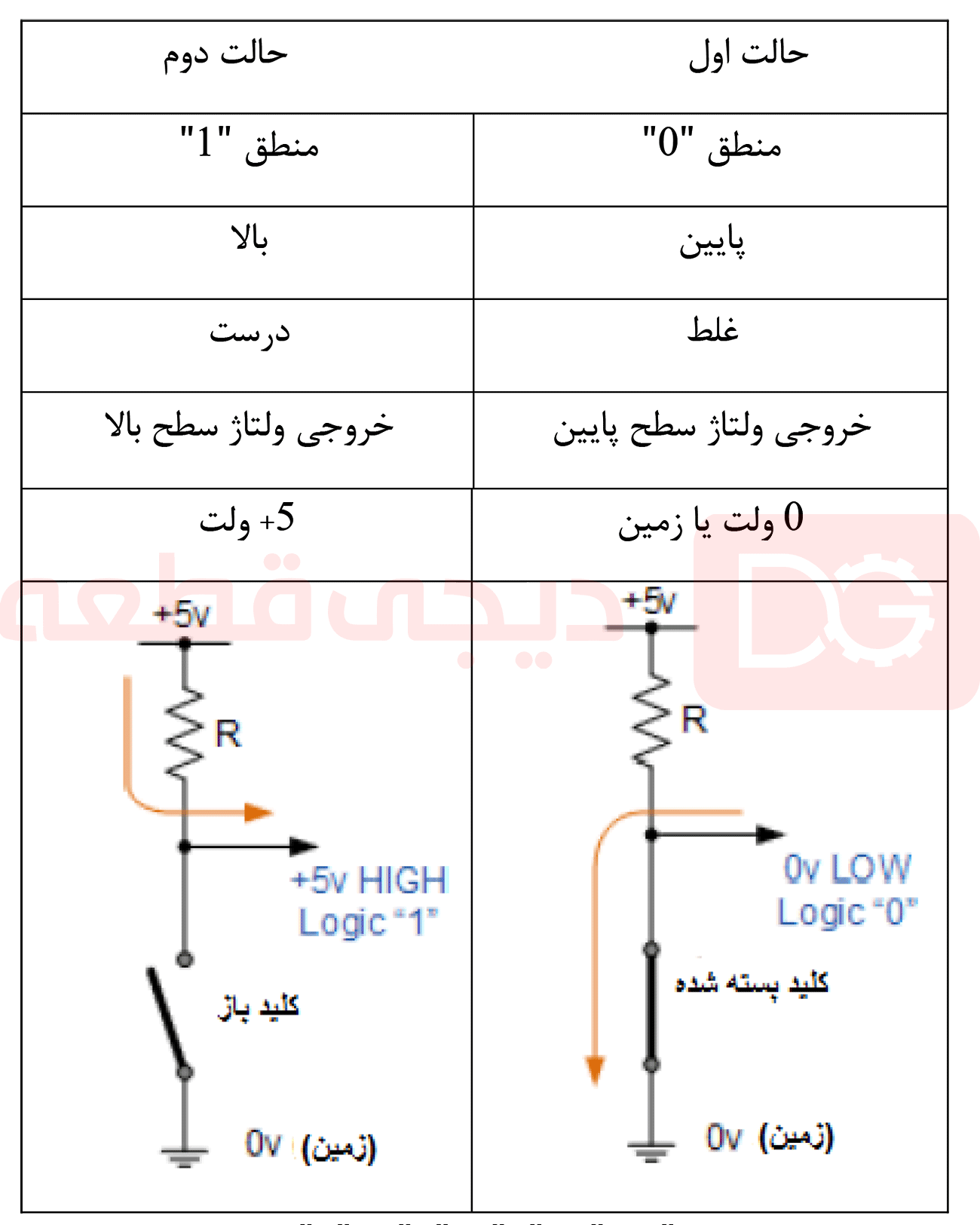
همچنین، هنگام تبدیل اعداد دودویی به ده دهی  یا حتی از ده دهی به دودویی، باید مراقب باشیم تا دو گروه از اعداد را با هم قاطی نکنیم. برای مثال، اگر ما رقم 10 را روی کاغذ می‌نویسیم آن می‌تواند به معنی “ده” باشد اگر فرض کنیم آن یک عدد ده دهی است، یا آن می‌تواند برابر با “1” و “0” باهم در دودویی باشد که برابر با عدد دو در قالب ده دهی وزن‌دار ذکر شده در بالا باشد.

یک راه برای غلبه بر این مشکل، هنگام تبدیل اعداد دودویی به ده دهی و برای تشخیص این که آیا ارقام یا اعدادی که استفاده می‌شوند ده دهی یا دودویی هستند، نوشتن یک عدد کوچک به نام “زیرنویس” بعد از اخرین رقم برای نشان دادن مبنای سیستم اعداد استفاده شده است.

بنابراین برای تبدیل اعداد دودویی به ده دهی به عنوان مثال، اگر از یک رشته عدد دودویی استفاده کنیم، برای نشان دادن عدد مبنای 2، باید زیر نویس “2”  را اضافه کنیم، بنابراین عدد بصورت 10₂ نوشته می شود. به همین ترتیب، اگر آن یک عدد اعشاری استاندارد باشد، ما باید برای نشان دادن عدد مبنای 10، زیر نویس 10 را اضافه کنیم، بنابراین این عدد به صورت 10₁₀ نوشته می‌شود.

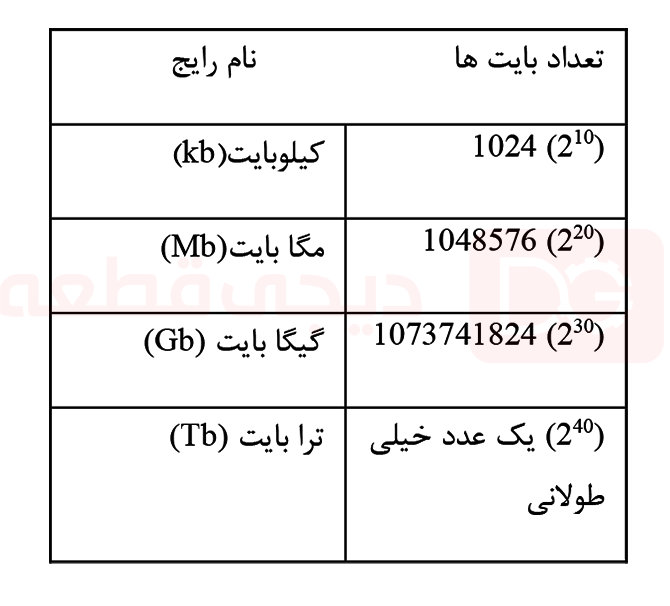
امروزه، از آنجا که سیستم های میکروکنترلر یا میکروپردازنده به طور فزاینده‌ای بزرگ شده‌اند، ارقام دودویی جداگانه (بیت) اکنون در 8 گروه برای تشکیل یک بایت واحد با یکدیگر جمع شده‌اند بطوریکه اندازه اکثر سخت افزارهای کامپیوتر مانند هارد دیسک ها و ماژول‌های حافظه در مگابایت یا حتی گیگابایت نشان داده می‌شود.

خلاصه تبدیل اعداد دودویی به ده دهی

“BIT” اصطلاح اختصاری است که از رقم دودویی گرفته شده است.

یک سیستم دودویی فقط دو حالت دارد، منطق “0” و منطق “1” که مبنای 2 را ارائه می‌دهند.

یک سیستم ده دهی از 10 رقم مختلف استفاده می‌کند، 0 تا 9 که بر مبنای 10 است.

یک شماره دودویی یک عدد وزن‌دار است که ارزش وزنی آن از راست به چپ افزایش می‌یابد.

وزن یک رقم دودویی از راست به چپ دو برابر می‌شود.

با استفاده از روش جمع وزن‌ها یا روش تقسیم بر 2 تکراری، می‌توان یک عدد دهدهی را به یک عدد دودویی تبدیل کرد.

وقتی اعداد را از دودویی به دهدهی یا از ده دهی به دودویی تبدیل می‌کنیم، از زیرنویس‌ها برای جلوگیری از خطا استفاده می‌شود.

تبدیل دودویی به ده دهی (مبنای-2 به مبنای- 10) یا اعداد ده دهی به دودویی (مبنای-10 به مبنای-2) می‌تواند به روش‌های مختلفی مانند شکل بالا انجام شود. هنگام تبدیل اعداد ده دهی به دودویی، مهم است که به یاد داشته باشید که کم اهمیت‌ترین بیت (LSB) و مهمترین بیت (MSB) است.

در آموزش بعدی در مورد منطق دودویی بر تبدیل اعداد دودویی به اعداد هگزا دسیمال و بر عکس خواهیم پرداخت و نشان می‌دهیم که اعداد دودویی می‌توانند توسط حروف  همانند اعداد نمایش داده شوند.

1. Most Significant Digit
2.  Least Significant Digit