اعداد هگزا دسیمال به زبان ساده 

اعداد هگزا دسیمال اعداد دودویی را در مجموعه‌های 4 تایی گرد می‌آورد و امکان تبدیل 16 رقم دودویی متفاوت را ممکن می‌سازد. یکی از اصلی‌ترین ضعف‌های اعداد دودویی این است که رشته اعداد دودویی معادل با یک اعداد مبنای 10 بزرگ می‌تواند کاملا طولانی باشد.

هنگام کارکردن با سیستم‌های دیجیتال بزرگ، مانند کامپیوترها، پیدا کردن اعداد دودویی متشکل از 8،16 و حتی 32 رقم که خواندن و نوشتن آن بدون تولید خطا سخت مخصوصا زمانی که با تعداد زیادی اعداد دودویی 16 یا 32 بیت کار می‌کنیم، معمول است.

اعداد هگزادسیمال

یک روش رایج غلبه بر این مشکل آرایش اعداد دودویی در گروه‌ها یا مجموعه‌هایی از چهار بیت (4- بیت) است. این گروه‌های 4 بیتی نوع دیگری از سیستم اعداد گذاری که همچنین رایجا در سیستم‌های دیجیتال و کامپیوتر که اعداد هگزا نامیده می‌شود، به کار می‌رود.

سیستم شماره‌گذاری “هگزا دسیمال” یا به سادگی “هگزا” سیستم مبنای 16 را به کار می‌برد و یک انتخاب معروف برای نمایش مقادیر دودویی طولانی  است زیرا که قالب آنها کاملا فشرده است و فهم آن در مقایسه با رشته‌های دودویی طولانی 1 ام و 0 ام آسانتر است.

یک سیستم مبنای 16، درنتیجه سیستم شماره‌گذاری هگزادسیمال 16 ارقام مختلف (شانزده) را با یک ترکیب از اعداد 0 تا 15 به کار می‌برد. در بیان دیگر، 16 نماد رقم ممکن وجود دارد.

اگرچه، یک مشکل بالقوه به کار بردن این روش در اعداد هگزا دسیمال، نام‌گذاری رقم بوجود آمده توسط این حقیقت که اعداد دسیمال 10،11،12،13،14 و 15 به صورت نرمال با استفاده از دو نماد مجاور نوشته شده‌اند، است. برای مثال  اگر 10 را در هگزادسیمال بنویسیم، منظور عدد دسیمال ده، یا عدد دودویی 2 (1+0) است . برای غلبه بر این مشکل اعدا هگزادسیمالی که مقادیر ده، یازده،…. پانزده را تعیین می‌کنند با حروف بزرگ A ,B ,C ,D ,E و F جایگزین می‌شوند.

سپس در سیستم شماره‌گذاری هگزادسیمال ما اعداد 0 تا 9 را به کار می‌بریم و حروف بزرگ A تا F تا معادل دودویی یا دسیمال آن را نشان دهیم، که با یک رقم کم اهمیت در بخش سمت راست شروع می‌شود.

همانطور که گفتیم، رشته‌های دودویی می‌تواند بسیار طولانی باشد و برای خواندن سخت است اما می‌توانیم ان را با استفاده از تقسیم این اعداد دودویی بزرگ به گروه‌هایی برای آسانتر کردن نوشتن و دانستن تبدیل کرد. برای مثال، گروه پیش رو ارقام دودویی 1101 0101 1100 1111₂ برای خواندن و دانستن بسیار آسانتر از 1101010111001111₂ است هنگامی که آنها با یکدیگر دسته‌بندی شده‌اند.

برای استفاده از سیستم شماره‌گذاری دسیمال، ما از گروه‌هایی 3 رقمی یا 000 ها از بخش سمت راست برای ایجاد یک عدد بسیار بزرگ مانند یک میلیون یا تریلیون استفاده می‌کنیم که فهم آن برای ما آسان است و همان برای سیستم‌های دیجیتال نیز درست است.

اعداد هگزادسیمال یک سیستم بسیار پیچیده نسبت به استفاده از تنها دودویی یا دسیمال است و اساسا هنگامی که با کامپیوترها و موقعیت آدرس‌های حافظه سرو کار داریم استفاده می‌شود. با تقسیم یک عدد دودویی به گروه‌های 4 بیتی، هر گروه یا مجموعه 4 رقمی اکنون می‌تواند دارای یک مقدار ممکن بین “0000”(0) و “1111” (8+4+2+1=15) باشد که یک مجموع 16 عدد متفاوت ترکیبی از 0 تا 15 است. فراموش نکنید که “0” همچنین  یک رقم معتبر است.

از اولین آموزش خود درباره اعداد دودویی به خاطر داریم که یک گروه 4 بیتی از ارقام یک “nibble” نامیده می‌شود و از آنجا که 4 بیت همچنین نیازمند تولید یک عدد هگزادسیمال است، یک رقم هگزا همچنین می‌توان به صورت یک تکه یا نصف یک بیت تصور شود. سپس دو عدد هگزادسیمال برای تولید یک بایت کامل از 00 تا FF نیاز است.

همچنین، از آنجا که 16 در سیستم دسیمال توان چهارم 2  ( یا 2⁴  )  یک رابطه مستقیم بین اعداد 2 و 16 وجود دارد بنابراین یک رقم هگزا دارای یک مقدار معادل با 4 ارقام دودویی چهار است بنابراین اکنون q معادل با “16” است.

به دلیل این رابطه، 4 رقم در یک عدد دودویی می‌تواند با یک رقم هگزادسیمال واحد نشان داده شود. این تبدیل بین اعداد دودویی و هگزادسیمال بسیار آسان است و هگزادسیمال می‌تواند برای نوشتن تبدیل اعداد دودویی بزرگ به ارقام بسیار پایین‌تر استفاده شود.

اعداد 0 تا 9 همچنان به عنوان سیستم دسیمال اصلی استفاده می‌شوند، اما اعداد از 10 تا 15 اکنون توسط حروف بزرگ الفبا از A تا F نشان داده شده‌اند و رابطه بین دسیمال، دودویی، و هگزادسیمال به صورت زیر ارائه شده است.

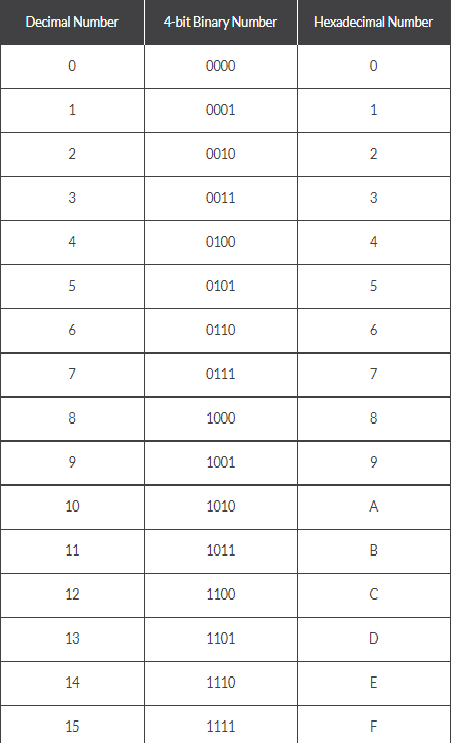
عدد دودویی اصلی از 1101 0101 1100 1111₂ بالا، این اکنون می‌تواند به یک عدد هگزادسیمال معادل D5CF که بسیار آسان‌تر برای خواندن و فهم نسبت به یک ردیف طولانی 1 ها و 0 ها که قبلا داشتیم، است.

بنابراین با استفاده از علامت‌گذاری هگزادسیمال، اعداد دیجیتال می‌تواند با استفاده از ارقام کمتر و با شباهت کمتر یک رخداد خطا می‌تواند نوشته شود. متشابها، تبدیل اعداد مبنای هگزادسیمال به دودویی به سادگی عملیات معکوس است.

سپس ویژگی‌های اصلی یک سیستم شماره‌گذاری هگزادسیمال این است که 16 رقم شمارش متمایز از 0 تا F با هر رقم که دارای  یک وزن یا مقدار 16 است که از کم اهمیت‌ترین بیت (LSB) شروع می‌شود. برای تمایز بین اعداد هگزادسیمال از اعداد دیناری، یک پیشوند “#” (هشتگ) یا یک “$” (علامت‌دار) قبل از مقدار عدد هگزادسیمال واقعی#D5CF  یا $D5CF  استفاده شده است.

از آنجا که پایه یک سیستم هگزادسیمال 16 است، که همچنین نشان دهنده عدد نمادهای مستقل استفاده شده در سیستم  است که زیرنویس 16 برای تعیین یک عدد بیان شده در هگزادسیمال به کار می‌رود. برای مثال، عدد هگزادسیمال قبلی به صورت : D5CF₁₆ بیان شده است.

شمارش با اعداد هگزادسیمال

بنابراین می‌دانیم چگونه 4 رقم دودویی را به یک عدد هگزادسیمال تبدیل کنیم. اما اگر بیش از 4 رقم دودویی داشتیم چگونه باید در هگزادسیمال در کنار کلمه نهایی F بشماریم. جواب ساده شروع دوباره با مجموعه دیگر از 4 بیت به صورت زیر است:

0…  …9, A,B,C,D,E,F, 10…to…19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21….

سردرگرم نباشید، 10 یا 20 ده یا بیست نیستند آن 1+0و 2+0 در هگزا دسیمال است. در حقیقت بیست حتی در هگزا وجود ندارد. با دو عدد هگزادسیمال می‌توان تا FF شمرد که معادل با دسیمال 255 است. به همین ترتیب، برای شمارش بالاتر از FF ما یک رقم هگزادسیمال سومی را به چپ اضافه می‌کنیم بنابراین اولین عدد هگزادسیمال 3 بیتی  برابر با 100₁₆ خواهد شد و آخرین برابر با FFF₁₆ (4095₁₀) خواهد شد. ماکزیمم عدد هگزادسیمال 4 رقمی FFFF₁₆ معادل با 65,535 در دسیمال و غیره است.

نمایش یک عدد هگزادسیمال

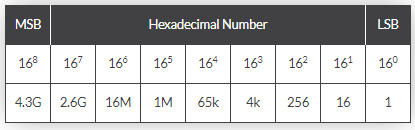
این اضافه کردن ارقام هگزادسیمال اضافی برای تبدیل هر دو اعداد دودویی و دسیمال به یک عدد هگزادسیمال بسیار آسان است اگر 4، 8،12 ا 16 رقم دودویی برای تبدیل باشد. اما همچنین می‌توان صفرهایی را به چپ مهمترین بیت MSB اگر عدد بیت‌های دودویی مضرب 4 نباشد است.

برای مثال، 11001011011001₂ یک عدد دودویی بیت چهارده است که برای تنها 3 رقم هگزادسیمال بزرگ است و برای یک عدد هگزادسیمال چهار بسیار کوچک است. جواب اضافه کردن صفر ها به بیت چپ ترین است تا زمانی که ما دارای یک مجموعه عدد 4 بیتی دودویی یا مضارب هستیم.

اضافه کردن 0 ها تا عدد دودویی اضافی

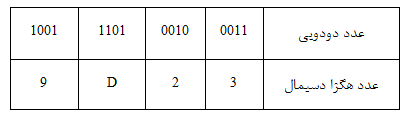
مزیت اصلی یک عدد هگزادسیمال این است که آن بسیار فشرده است و با استفاده از یک مبنای 16 به این معنی که تعداد رقم‌ها استفاده شده برای نمایش عدد داده شده معمولا کمتر از در دودویی یا دسیمال است. همچنین، آن سریع است و برای تبدیل بین اعداد هگزادسیمال و دودویی آسان است.

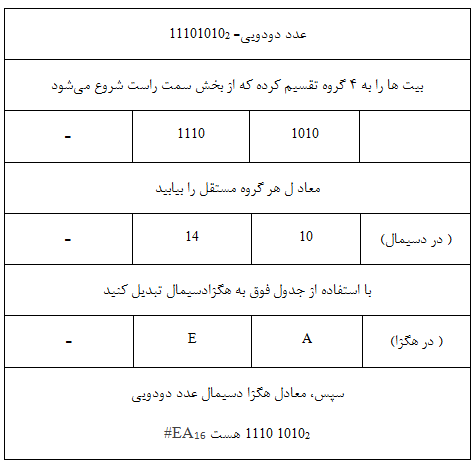
مثال شماره 2 اعداد هگزا دسیمال

عدد هگزا دسیمال #3FA7₁₆  را به معادل دودویی خود تبدیل کنید و همچنین به معادل دسیمال یا دیناری با استفاده از زیر نویس ها برای تعیین هر سیستم شماره‌گذاری تبدیل کنید.

#3FA7₁₆= 0011 1111 1010 0111₂=(8192 + 4096 + 2048 + 1024 + 512 + 256 + 128 + 32 + 4 + 2 + 1)= 16,295₁₀

سپس، عدد دسیمال 16295 می‌تواند به صورت زیر بیان شود:

#3FA7₁₆      در هگزادسیمال

                                                              یا

0011 1111 1010 0111₂ در دودویی

خلاصه اعداد هگزا دسیمال

هگزادسیمال یا Hex، سیستم شماره‌گذاری است که رایجا در سیستم‌های کامپیوتری و دیجیتال برای کاهش رشته‌های اعداد دودویی به یک مجموعه‌ای از 4 رقم برای درک آسان استفاده می‌شود. کلمه “هگزا دسیمال” به معنی 16 است زیرا که این نوع از سیستم شماره‌گذاری دیجیتال  از 16 رقم مختاف از 0 تا 9 و A تا F استفاده می‌کند.

برای تبدیل اعداد دودویی به اعداد هگزادسیمال در ابتدا باید عدد دودویی را به یک کلمه دودویی 4 بیتی که می‌تواند دارای هر مقدار از (00002)010 تا (11112)1510  که نشاندهنده معادل هگزادسیمال 0 تا F است تقسیم کنیم.