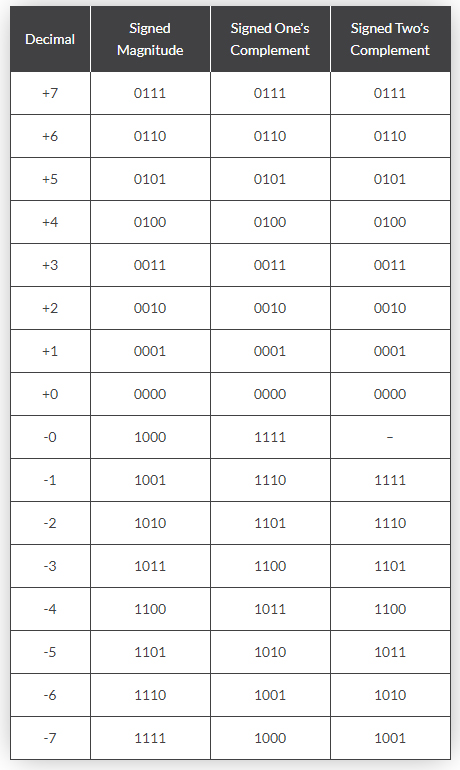
اعداد دودویی امضا شده 

اعداد دودویی امضا شده از MSB به عنوان یک بیت علامت برای نمایش طیف وسیعی از اعداد مثبت یا اعداد منفی استفاده می‌کنند.

اعداد علامت دار باینری

در ریاضیات، اعداد مثبت (شامل صفر) به عنوان اعداد بدون علامت نمایش داده می‌شوند. برای این است که ما علامت ve+ در جلوی آن برای نمایش اینکه آنها اعداد مثبت هستند قرار نمی‌دهیم.

با این حال، هنگام پرداختن به اعداد منفی، ما از علامت ve- در مقابل عدد استفاده می‌کنیم تا نشان دهیم مقدار عدد منفی است و با مقدار غیر علامت دار مثبت متفاوت است و در مورد اعداد دودویی علامت دار نیز همین امر وجود دارد.

با این حال، در مدارهای دیجیتال برای قرار دادن علامت مثبت یا منفی بر روی یک عدد هیچ گونه پیش بینی نشده است، زیرا سیستم های دیجیتال با اعداد دودویی کار می کنند که با “0” و “1” نشان داده می‌شوند. این “1 ها” و “0 ها” که با هم در میکروالکترونیک استفاده می شوند، بیت (در واقع ادغام رقم دودویی) نامیده می‌شوند، در اندازه های مختلفی از اعداد قرار می‌گیرند که با نام های مشترک مانند یک بایت یا یک کلمه ذکر می‌شوند.

اعداد دودویی

ما قبلاً نیز دیدیم که یک عدد باینری 8 بیتی (یک بایت) می تواند مقداری از 0 (00000000₂) تا 255 (11111111₂) داشته باشد، یعنی 256 = 2⁸ ترکیب مختلف بیت که یک بایت واحد 8 بیتی تشکیل می‌دهند. بنابراین به عنوان مثال یک عدد باینری بدون علامت مانند: 01001101₂ = 64 + 8 + 4 + 1 = 77₁₀ به صورت اعشاری. اما سیستم های دیجیتال و رایانه ها همچنین باید بتوانند از اعداد منفی همانند اعداد مثبت استفاده استفاده کنند.

جمع و تفریق اعداد علامت دار باینری

اعداد ریاضی عموماً از یک علامت و یک مقدار (بزرگی) تشکیل شده اند که در آن علامت مثبت(+) یا منفی بودن (-) عدد با مقداری که نشانگر اندازه عدد است را نشان می‌دهد، به عنوان مثال 23، 156+ یا 274- ارائه اعداد به این شکل، نمایش “علامت-اندازه” است زیرا از بیشترین رقم سمت چپ می‌تواند برای نشان دادن علامت و ارقام باقی مانده اندازه یا مقدار آن عدد استفاده کرد.

علامت – اندازه  یکی از متداول ترین و ساده ترین روش های نمایش اعداد مثبت و منفی در دو طرف صفر (0) است. بنابراین اعداد منفی به سادگی با تغییر علامت عدد مثبت متناظر بدست می آیند زیرا هر عدد مثبت یا بدون علامت مخالف علامت گذاری شده ای دارد، برای مثال، 2+ و 2- ، 10+ و 10 – و غیره.

اما اگر تعداد کل چیزی که داریم  یک مجموعه از صفرها و یک ها باشد، چگونه اعداد باینری علامت دار شده را نشان دهیم. ما می دانیم که رقم های باینری یا بیت ها فقط دو مقدار دارند، “1” یا “0” و به راحتی برای ما ، یک علامت نیز فقط دارای دو مقدار ، “+” یا “-” است.

سپس می‌توانیم با استفاده از یک بیت تنها یک عدد باینری علامت دار شده را مثبت یا منفی بدانیم. بنابراین برای نشان دادن یک عدد دودویی مثبت (n+) و یک عدد دودویی منفی (n-) ، می توانیم آنها را با اضافه کردن علامت استفاده کنیم.

جمع و تفریق اعداد منفی و مثبت

برای اعداد دودویی علامت دار شده از مهمترین بیت (MSB) به عنوان بیت علامت استفاده می‌شود. اگر بیت علامت “0” باشد، این به این معنی است که عدد از نظر مقدار مثبت است. اگر بیت علامت “1” باشد، عدد از نظر مقدار منفی است. بیت های باقیمانده در عدد برای نشان دادن مقدار عدد باینری به روش معمول تعداد باینری بدون علامت استفاده می‌شود.

سپس می توان دید که علامت – اندازه ¹(SM) با تقسیم بیت های کلی “n” به دو قسمت مقادیر مثبت و منفی را ذخیره می کند: 1 بیت برای علامت و n-1 بیت برای مقدار که یک عدد باینری خالص است. به عنوان مثال، عدد اعشاری 53 را می توان به عنوان یک عدد باینری 8 بیتی علامت دار شده به شرح زیر بیان کرد.

اعداد دودویی علامت دار مثبت

اعداد دودویی علامت دار منفی

نقطه ضعف در اینجا این است که در حالی که پیش از این ما یک عدد باینری بدون علامت بدون بیت با دامنه کامل n بیت داشتیم، اکنون یک عدد باینری علامت دار شده با n-1 بیت داریم که محدوده رقمی کاهش یافته بصورت زیر را ارئه می‌دهد:

                                                                                      -2^(n-1)  به   +2^(n-1)

بنابراین به عنوان مثال: اگر 4 بیت برای نمایش یک عدد باینری علامت دار شده داشته باشیم، (1 بیت برای بیت علامت و 3 بیت برای بیت اندازه)، در این صورت محدوده واقعی اعدادی که می توانیم در علامت گذاری- بزرگی نشان دهیم:

                                                                            -2^(4-1) – 1    به    +2^(4-1) – 1

                                                                               -2⁽³⁾ – 1    به    +2⁽³⁾ – 1

                                                                                           -7    به   +7

در حالی که پیش از این، محدوده یک عدد باینری 4 بیتی بدون علامت از 0 تا 15 یا 0 تا F در هگزادسیمال بود، اکنون ما یک محدوده کاهش یافته از 7- تا 7+ داریم. بنابراین یک عدد باینری بدون علامت یک بیت علامت واحد ندارد و بنابراین می تواند دامنه باینری بیشتری داشته باشد زیرا مهمترین بیت (MSB) فقط یک بیت یا رقم اضافی است تا بیت علامت استفاده شده.

یکی دیگر از معایب فرم شکل علامت این است که می توانیم برای صفر، 0 +یا 0000₂ و برای صفر ، 0 -یا 1000₂ داشته باشیم. هر دو معتبر هستند اما کدام یک صحیح است.

مثال شماره 1 اعداد دودویی علامت دار

مقادیر اعشار زیر را با استفاده از قالب اندازه – علامت به اعداد دودویی علامت دار شده تبدیل کنید:

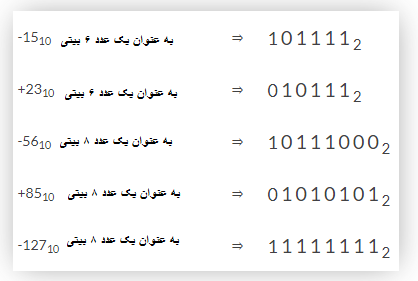
توجه داشته باشید که برای یک عدد دودویی علامتدار شده 4 بیتی، 6 بیتی ، 8 بیتی ، 16 بیتی یا 32 بیتی ، همه بیت ها باید یک مقدار داشته باشند، بنابراین “0” برای پر کردن فاصله بین بیت علامت سمت چپ و اولین یا بالاترین مقدار “1” استفاده می‌شود.

نمایش مقدار علامت یک عدد دودویی یک روش ساده برای استفاده و درک برای نمایش اعداد دودویی علامت دار شده است، زیرا ما همیشه از این سیستم با اعداد اعشاری عادی (پایه 10) در ریاضیات استفاده می‌کنیم. اگر عدد باینری منفی است یک “1” اضافه کنید و اگر مثبت است “0” اضافه کنید.

اگرچه، استفاده از این روش بزرگی علامت می‌تواند منجر به احتمال وجود دو الگوی بیت متفاوت با مقدار باینری یکسان شود. به عنوان مثال، 0+و 0- به ترتیب 0000 و 1000 به عنوان یک عدد باینری 4 بیتی علامت دار شده است. بنابراین می‌توان دریافت که با استفاده از این روش دو نمایش برای صفر، یک صفر مثبت (0000₂) و همچنین یک صفر منفی (1000₂) وجود دارد که می تواند عوارض بزرگی برای رایانه ها و سیستم های دیجیتال ایجاد کند.

اولین مکمل عدد باینری امضا شده

اولین مکمل، روش دیگری است که می توانیم برای نمایش اعداد دودویی منفی در یک سیستم اعداد باینری علامت دار شده استفاده کنیم. در اولین مکمل، اعداد مثبت (که به نام غیر مکمل نیز شناخته می شوند) مانند قبل با اعداد علامت – بزرگی بدون تغییر باقی می‌مانند.

با این حال، اعداد منفی با گرفتن مکمل یک (وارونگی، نفی) عدد مثبت بدون علامت نشان داده می شوند. از آنجا که اعداد مثبت همیشه با “0” شروع می شوند ، مکمل همیشه با “1” شروع می شود تا عدد منفی را نشان دهد.

مکمل یک عدد دودویی منفی مکمل همتای مثبت آن است، بنابراین برای گرفتن مکمل یک عدد دودویی، تنها کاری که باید انجام دهیم تغییر هر بیت به نوبه خود است. بنابراین مکمل “1” یک “0” است و برعکس، سپس مکمل 10010100₂ به سادگی 01101011₂ است زیرا همه 1 به 0 و 0 به 1 تغییر می‌یابد.

ساده ترین راه برای یافتن مکمل یک عدد دودویی علامت دار شده در هنگام ساخت مدارهای دیجیتال حساب یا رمزگشای منطقی، استفاده از اینورترها است. اینورتر به طور طبیعی یک مولد مکمل است و می توان به طور موازی از آن برای یافتن مکمل 1 از هر عدد دودویی همانطور که نشان داده شده استفاده کرد.

مکمل 1 با استفاده از مبدل ها

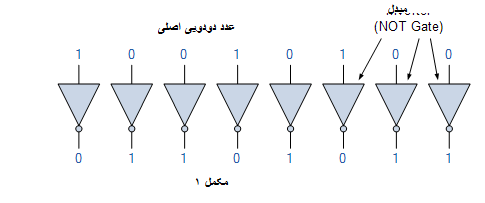
سپس می توان دید که یافتن مکمل یک عدد باینری N بسیار آسان است، زیرا تمام آنچه را که باید انجام دهیم این است که به سادگی 1 ها را به 0 و 0 را به 1 تغییر دهیم تا معادل N – را به ما بدهد. همچنین دقیقاً مانند نمایش قبل بزرگی علامت، مکمل یک نیز می تواند دارای علامت n-bit باشد تا اعداد را در محدوده: -2^(n-1) و+2^(n-1) – 1 نشان دهد. به عنوان مثال،  نمایش 4 بیتی در قالب مکمل یک می تواند برای نشان دادن اعداد اعشاری در بازه از 7-تا 7+با دو نمایش از صفر  بکار رود: 0000 (0+) و 1111 (0-) همانند شکل قبلی.

جمع و تفریق با استفاده از مکمل یک

یکی از اصلی ترین مزایای مکمل یک در جمع و تفریق دو عدد باینری است. در ریاضیات، تفریق را می توان از طرق مختلف به صورت A – B اجرا کرد ، همانند اینکه بگوییم A + (-B) یا -B + A و غیره است. بنابراین، اختلال کسر دو عدد باینری را می توان به سادگی با استفاده از جمع انجام داد.

ما در آموزش جمع دودویی دیدیم که جمع دودویی از همان قوانینی که برای جمع عادی دارد پیروی می کند با این تفاوت که در باینری فقط دو بیت (رقم) وجود دارد و بزرگترین رقم “1” است (همانطور که “9” بزرگترین است رقم اعشاری) بنابراین ترکیبات احتمالی برای جمع دودویی به شرح زیر است:

وقتی هر دو عدد جمع شده مثبت باشند، جمع A + B ، می توان آنها را با استفاده از جمع مستقیم (شامل عدد و بیت علامت) جمع کرد، زیرا وقتی تک بیت ها با هم جمع می شوند، “0 + 0” ، “0 + 1” یا “1 + 0” منجر به جمع “0” یا “1” می‌شود. این به این دلیل است که وقتی دو بیتی که می‌خواهیم با هم جمع شوند زوج هستند (“0” + “1” یا “1 + 0”) ، نتیجه “1” می شود. به همین ترتیب وقتی دو بیتی که جمع شود ، فرد باشند (“0 + 0” یا “1 + 1”) نتیجه “0” است تا زمانی که به “1 + 1” برسیم، سپس حاصل جمع برابر با “0”  به اضافه “1” است . بیایید به یک مثال ساده نگاه کنیم.

تفریق دو عدد دودویی

یک سیستم دیجیتالی 8 بیتی لازم است تا دو عدد 115 و 27 زیر را با استفاده از مکمل یکاز یکدیگر کم کند. بنابراین به صورت اعشاری این مقدار خواهد بود: 115 – 27 = 88.

ابتدا باید دو عدد اعشاری را به باینری تبدیل کنیم و مطمئن شویم که با اضافه کردن صفرهای پیش رو برای تولید یک عدد 8 بیتی (بایت)  هر عدد تعداد بیت های یکسانی را دارد. از این رو:

                                                                            115₁₀  در دودویی:  01110011₂

                                                                            27₁₀  در دودویی:  00011011₂

حال باید مکمل عدد باینری دوم، (00011011) را پیدا کنیم در حالی که عدد اول (01110011) را بدون تغییر باقی می گذاریم. بنابراین با تغییر همه 1 به 0 و 0 به 1 ، مکمل یک 00011011 برابر 11100100 است.

با اضافه کردن عدد اول و متمم عدد دوم:

از آنجایی که سیستم دیجیتال با 8 بیت کار می کند ، فقط هشت رقم اول برای ارائه پاسخ جمع استفاده می شود و ما به راحتی آخرین بیت (بیت 9) را نادیده می گیریم. این بیت یک بیت “سرریز” است. سرریز وقتی اتفاق می افتد که حاصل جمع مهمترین (چپ ترین) ستون ، یک انتقال به جلو ایجاد کند. این بیت سرریز یا بار را می توان به طور کامل نادیده گرفت یا به قسمت دیجیتال بعدی منتقل کرد تا در محاسبات از آن استفاده شود. سرریز نشان دهنده مثبت بودن پاسخ است. اگر سرریز وجود نداشته باشد، پاسخ منفی است.

8 بیت حاصل از بالا: 01010111 (سرریز “1” لغو می شود) و برای تبدیل آن از یک پاسخ مکمل یک به پاسخ واقعی، اکنون باید “1” را به نتیجه مکمل یک اضافه کنیم، بنابراین:

بنابراین نتیجه تفریق 27 (00011011₂) از 115 (01110011₂) با استفاده از مکمل 1 در باینری جواب زیر را می دهد: 01011000₂ یا (64 + 16 + 8) = 88₁₀به صورت اعشاری.

سپس می‌توان دریافت که اعداد باینری علامت دار شده یا بدون علامت را می توان با استفاده از مکمل یک و روند جمع از یکدیگر کم کرد. از جمع کننده های باینری مانند TTL 74LS83 یا LS283 74می توان برای جمع یا تفریق دو عدد دودویی 4 بیتی علامت دار شده و یا با هم بصورت سری استفاده کرد و جمع کننده های 8 بیتی کامل تولید کرد.

دومین مکمل عدد دودویی علامت دار

مکمل دوم یا به اصطلاح دومین مکمل، روش دیگری مانند اندازه – علامت قبلی و فرم مکمل قبلی است که می توانیم از آن برای نمایش اعداد دودویی منفی در سیستم اعداد باینری علامت دار شده استفاده کنیم. در مکمل دو، اعداد مثبت دقیقاً مانند اعداد باینری بدون علامت هستند. با این حال، یک عدد منفی با یک عدد دودویی نشان داده می شود که اگر به معادل مثبت مربوطه اضافه شود، صفر می‌شود.

در فرم مکمل دو، یک عدد منفی مکمل 2 عدد مثبت آن است که دو عدد از آن کم می شود A –  A – B = A + مکمل 2 B ) با استفاده از همان فرایند قبلی به طور اساسی ، مکمل دو مکمل یک به اضافه یک است.

مزیت اصلی مکمل دو نسبت به مکمل قبلی این است که مشکلی دو برابر صفر وجود ندارد به علاوه تولید مکمل دو عدد دودویی علامت دار شده بسیار آسان تر است. بنابراین، هنگامی که اعداد در قالب مکمل دو نشان داده می شوند، انجام عملیات حساب نسبتاً آسان تر است.

بیایید به تفریق دو عدد 8 بیتی 115 و 27 خود از بالا با استفاده از مکمل دو نگاه کنیم و از بالا به یاد می آوریم که معادل های باینری عبارتند از:

                                                                                   115₁₀  در باینری:  01110011₂

                                                                                  27₁₀   در باینری:  00011011₂

اعداد ما 8 بیت طول دارند ، سپس 2⁸ رقم موجود برای نشان دادن مقادیر ما وجود دارد ودر باینری این برابر است با 100000000₂ یا 256₁₀. سپس مکمل دو 27₁₀ خواهد بود:

                                                              (2⁸)₂ – 00011011 = 100000000 – 00011011 = 11100101₂

مکمل عدد منفی دو به این معنی است که تفریق جمع بسیار ساده تری از دو عدد می شود بنابراین جمع برابر با:  (مکمل2 عدد 27)+115که عبارت است با:

                                                                       01110011 + 11100101 = 1 01011000₂

همانند قبل، بیت سرریز 9 نادیده گرفته می شود زیرا ما فقط به 8 بیت اول علاقه مند هستیم، بنابراین نتیجه برابر: 01011000₂ یا (64 + 16 + 8) = 88₁₀ بصورت اعشاری هماند شکل قبلی است.

خلاصه اعداد دودویی علامت دار

دیدیم که اعداد دودویی منفی را می توان با استفاده از مهمترین بیت (MSB) به عنوان بیت علامت نشان داد. اگر یک عدد باینری n بیت علامت دار شود، از بیت چپ برای نشان دادن علامت استفاده می شود که n-1 بیت را نشان می دهد.

به عنوان مثال، در یک عدد باینری 4 بیتی، این فقط 3 بیت باقی می گذارد تا شماره واقعی را نگه دارد. اگر با این وجود، عدد باینری علامت دار نشده است، می توان از همه بیت ها برای نشان دادن عدد استفاده کرد.

نمایش عدد دودویی علامت دار شده معمولاً به عنوان علامت علامت- اندازه نشان داده می شود و اگر بیت علامت “0” باشد، عدد مثبت است. اگر بیت علامت “1” باشد، عدد منفی است. هنگام پرداختن به عملیات ریاضی دودویی، استفاده از مکمل عدد منفی راحت تر است.

تکمیل یک روش جایگزین برای نمایش اعداد دودویی منفی است. این سیستم کدگذاری جایگزین امکان تفریق اعداد منفی را با استفاده از جمع ساده فراهم می کند.

از آنجا که اعداد با علامت مثبت همیشه با یک صفر (0) شروع می شوند، بنابراین مکمل آن همیشه با یک (1) شروع می شود تا یک عدد منفی نشان داده شود که در جدول زیر نشان داده شده است.

مقایسه عدد باینری علامت دار شده 4 بیتی