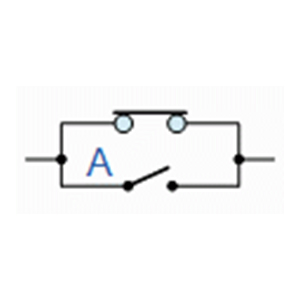
جبر بولی از مجموعه ای از قوانین برای تعریف عملکرد مدار منطق دیجیتالی استفاده میکند. همانطور که از نمادهای منطقی “0” و “1” برای نشان دادن استفاده میشود، ما نیز می توانیم از آنها به ترتیب برای “باز” یا “بسته” شدن مدار یا کلید استفاده کنیم.
فهرست مطالب
قوانین جبر بولی
مجموعه ای از قوانین یا قوانین عبارات جبر بولی برای کمک به کاهش تعداد گیت های منطقی مورد نیاز برای انجام یک عملیات منطقی خاص و در نتیجه لیستی از توابع یا قضیه ها که به عنوان قوانین جبر بولی شناخته می شوند، اختراع شده است.
جبر بولی ریاضیاتی است که ما برای تحلیل گیت ها و مدارهای دیجیتال استفاده می کنیم. ما می توانیم از این “قوانین بولی” برای کاهش و ساده سازی عبارت پیچیده بولی در تلاش برای کاهش تعداد گیت های منطقی مورد نیاز استفاده کنیم. بنابراین جبر بولی سیستمی از ریاضیات مبتنی بر منطق است که مجموعه قوانین یا قوانینی خاص خود را دارد که برای تعریف و کاهش عبارات بولی استفاده میشود.
قوانین جبر بول در مدار منطقی
متغیرهای مورد استفاده در جبر بولی فقط یکی از دو مقدار ممکن را دارند، یک منطق “0” و یک منطق “1” اما یک عبارت می تواند تعداد بی نهایت متغیری داشته باشد که همه آنها به صورت جداگانه برچسب گذاری شده اند و ورودی های عبارت را نشان میدهند، به عنوان مثال، متغیرهای A ، B ، C و غیره که به ما یک عبارت منطقی از A + B = C می دهد، اما هر متغیر تنها می تواند 0 یا 1 باشد.
نمونه هایی از این قوانین فردی بولی، قواعد و قضیه های جبر بولی در جدول زیر آورده شده است.
جدول درستی قوانین بولی
| بیان بولی | توضیحات | مدار سوئیچینگ معادل | قانون جبر بولی |
| A + 1 = 1
|
سوئیچ A موازی بسته=
” بسته” |
  |
لغو |
| A + 0 = A
|
سوئیچ A موازی باز=
” A “ |
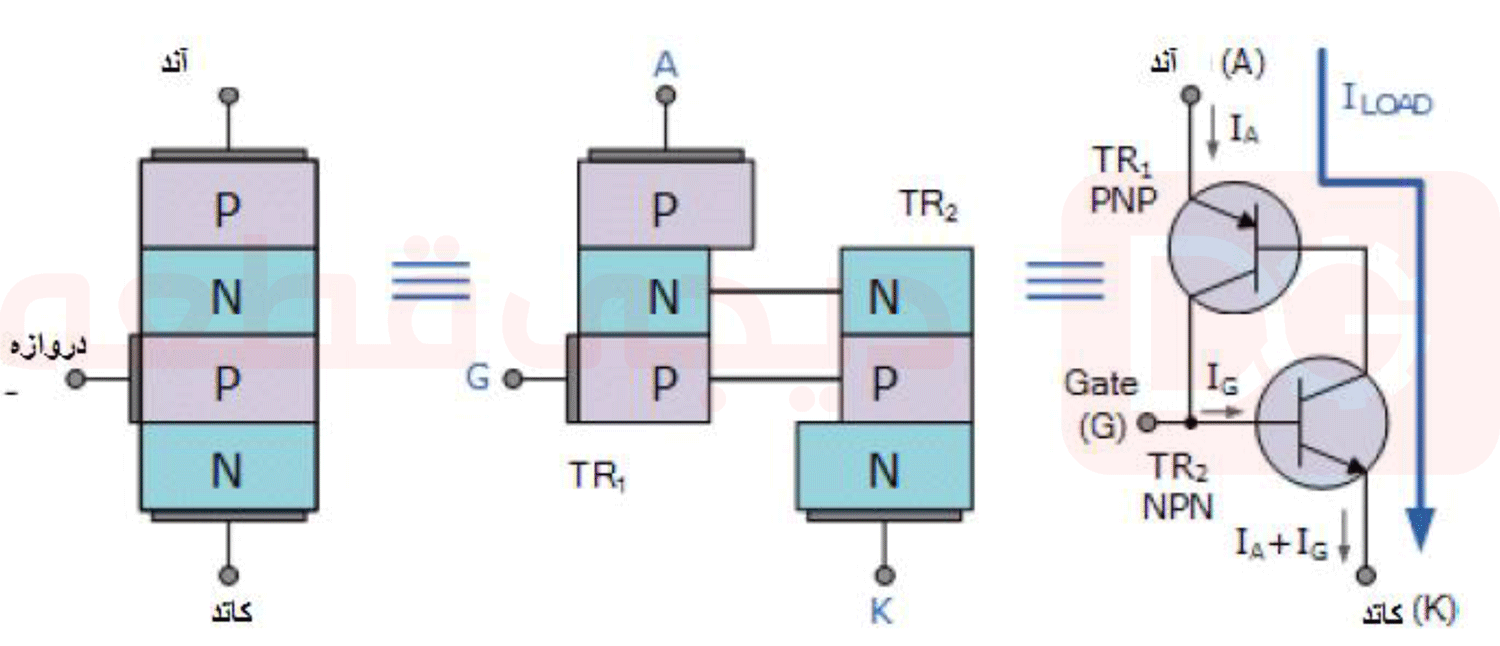  |
شناسایی |
| A . 1 = A
|
A سری با بسته =
“A” |
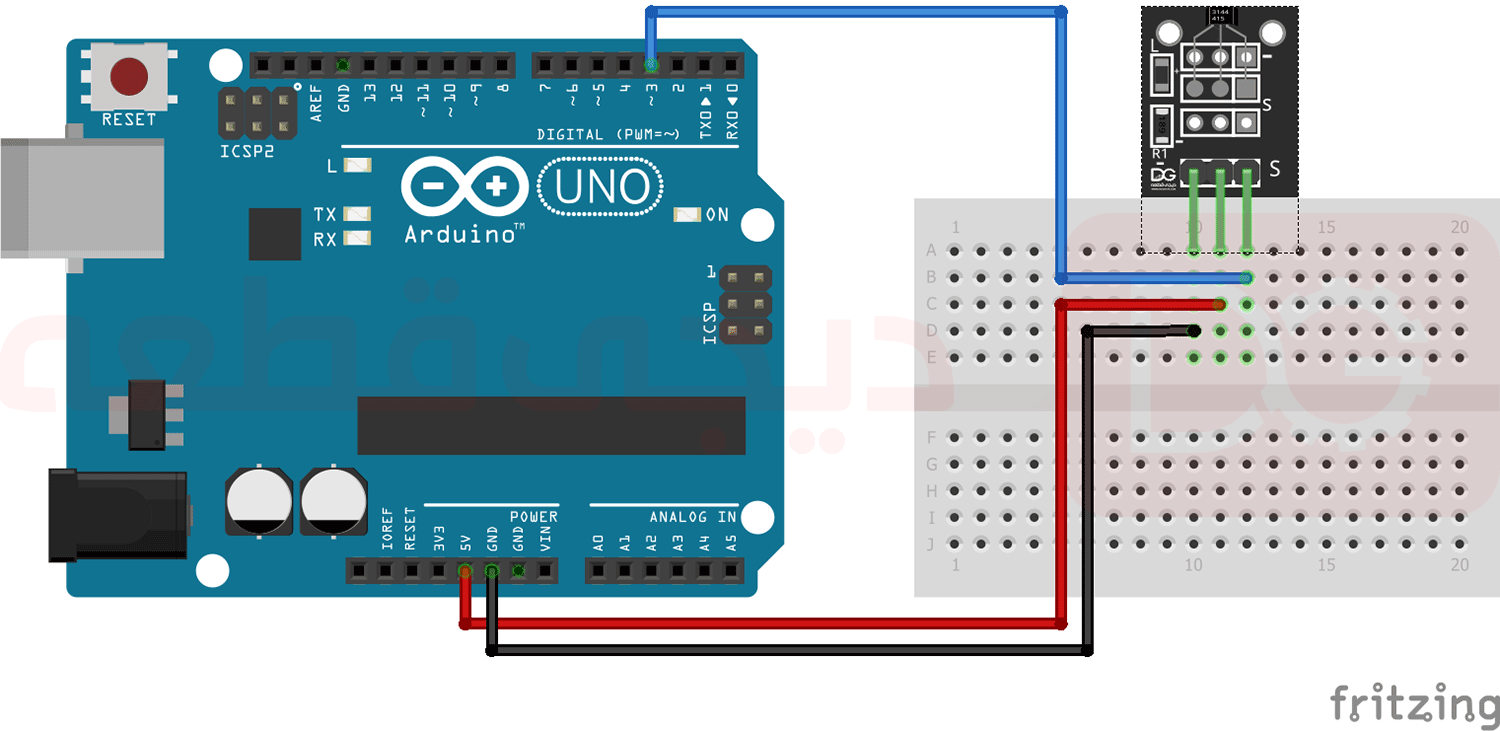  |
شناسایی |
| A . 0 = 0
|
A سری با باز=
“باز” |
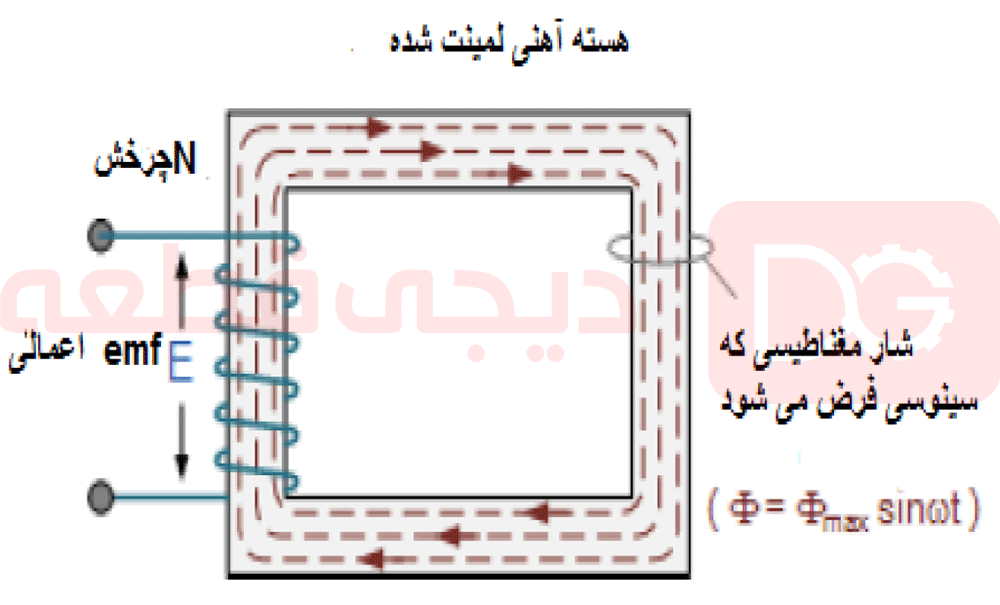   |
لغو |
| A + A = A
|
A موازی با A=
“A “ |
بی توان | |
| A . A = A
|
A سری با A=
“A” |
بی توان | |
| NOT = A
|
NOT NOT A
( منفی دوبل) = “A” |
منفی دوتایی | |
| A + = 1
|
A موازی با NOT A=
” بسته” |
   |
مکمل |
| A . A = 0
|
A سری با NOT A=” باز” |   |
مکمل |
| A+B = B+A
|
A موازی با B =
B موازی با A |
  |
جابجایی |
| A.B = B.A
|
A سری با B =
B سری با A |
  |
جابجایی |
| =
|
OR معکوس شده و جابه جا شده با AND | قضیه دمورگان | |
| = +
|
AND معکوس شده و جابجا شده باOR | قضیه دمورگان |
قوانین اساسی جبر بولی که مربوط به قانون جابجایی است، اجازه تغییر در موقعیت برای جمع و ضرب را می دهد، قانون تداعی اجازه حذف براکت ها را برای جمع و ضرب را می دهد، و همچنین قانون توزیعی که فاکتور بندی یک عبارت را مجاز می داند، که همانند مواردی است که در جبر معمولی وجود دارد.
هر یک از قوانین بولی در بالا فقط با یک یا دو متغیر آورده شده است، اما تعداد متغیرهای تعریف شده توسط یک قانون محدود به این نمی شود زیرا تعداد بی نهایت متغیر به عنوان ورودی نیز بیان میشود. این قوانین بولی که در بالا توضیح داده شده است میتواند برای اثبات هر عبارت بولی و همچنین ساده سازی مدارهای دیجیتالی پیچیده استفاده شود.
شرح مختصری از قوانین مختلف بولی در زیر آورده شده است که A نشان دهنده ورودی متغیر است.
اثبات قضایای جبر بول
قانون لغو – اصطلاحA AND شده با “0” برابر با 0 یا OR شده با “1” برابر با 1 خواهد بود
A.0=0 A AND شده با 0 همیشه برابر با 0 است.
A + 1 = 1 A OR شده با 1 همیشه برابر با 1 است.
قانون هویت – A OR شده با “0” یا AND شده با یک “1” همیشه با این اصطلاح برابر است.
A + 0 = A : متغیر A OR شده با 0 همیشه معادل با متغیر خواهد بود.
A.1=A : متغیر A AND شده با 1 همیشه برابر با متغیر است.
قانون موقت- ورودی که با خودش AND یا OR شود برابر با آن ورودی است
A + A = A یک متغیر OR شده با خود همیشه برابر با متغیر است.
A . A = A یک متغیر AND شده با خود همیشه برابر با متغیر است.
قانون متمم – A AND شده با مكمل آن برابر با “0” و اصطلاح OR شده با مكمل آن برابر با “1” است.
0=A AND : شده با مکمل خود همیشه برابر با 0 است.
A + = 1 : A OR شده با مکمل خود همیشه برابر با 1 است.
قانون جابجایی – ترتیب کاربرد دو اصطلاح جداگانه مهم نیست.
A.B=B.A ترتیب دو متغیر AND شده هیچ تفاوتی ایجاد نمی کند.
A + B = B + A ترتیب قرار گرفتن دو متغیر در OR هیچ تفاوتی ندارد.
قانون منفی دوبل – اصطلاحی که دو بار معکوس شود برابر با اصطلاح اصلی است
A= مکمل مضاعف یک متغیر همیشه برابر با متغیر است.
قضیه دمورگان- دو قاعده یا قضیه ” دمورگان” وجود دارد.
(1) دو اصطلاح جداگانه NOR شده با هم همان دو اصطلاح معکوس (متمم) و AND شده است به عنوان مثال:
[latexpage]
[
:= bar{A.B} bar{A+B}
]
(2) دو اصطلاح جداگانه NAND شده با هم همان دو اصطلاح معکوس (متمم) و OR شده است به عنوان مثال:
[latexpage]
[
bar{A.B}=bar{A}+bar{B}
]
سایر قوانین جبری بولی که در بالا جزئیات آن ذکر نشده است عبارتند از:
مفروضات بولی – گرچه در نوع خود قوانین بولی نیستند، اما اینها مجموعه ای از قوانین ریاضی هستند که می توانند در ساده سازی عبارات بولی استفاده شوند.
0.0=0 ،0 ضرب شده با خود همیشه برابر با 0 است.
1.1=1 ،1 ضرب شده با خود همیشه معادل 1 است.
1.0=0 ،1 ضرب شده با 0 معادل 0 است.
0+0=0 یک 0 OR شده با خود همیشه معادل 0 است.
1 + 1 = 1 ،OR شده با خودش همیشه برابر با 1 است.
1 + 0 = 1 ،OR شده با 0 برابر با 1 است.
وارون (متمم) 1 همیشه برابر با 0 است.
(متمم) 0 همیشه برابر با 1 است.
قانون توزیعی – این قانون ضرب یا فاکتور گرفتن از یک عبارت را مجاز می داند.
A (B + C) = A.B + A.C (OR قانون توزیعی)
A + (B.C) = (A + B). (A + C) (AND) : AND) قانون توزیعی)
قانون جذب – این قانون با جذب اصطلاحات مشابه، بیان پیچیده را به عبارت ساده تر کاهش می دهد.
A + (A.B) = (A.1) + (A.B) = A (1 + B) = A (یا قانون جذب)
A (A + B) = (A + 0). (A + B) = A + (0.B) = A (و قانون جذب)
قانون تداعی – این قانون اجازه می دهد تا براکت ها را از یک عبارت حذف کرده و مجدداً متغیرها را دسته بندی مجدد کنید.
A + (B + C) = (A + B) + C = A + B + C (یا قانون وابسته)
A (B.C) = (A.B) C = A. ب C (و قانون پیوسته)
توابع جبر بولی
با استفاده از اطلاعات بالا، گیت های 2 ورودی AND ، OR و NOT ساده با 16 توابع ممکن نشان داده می شوند ،که در جدول زیر نشان داده شده است.
| تابع | شرح | بیان |
| 1 | تهی | 0 |
| 2 | هویت | 1 |
| 3 | ورودی A | A |
| 4 | ورودی B | B |
| 5 | NOT A
|
[latexpage] [ bar{A} ] |
| 6 | NOT B |
[latexpage] [ bar{B} ] |
| 7 | A AND B (AND) |
[latexpage] [ A . B ] |
| 8 | A AND NOT B |
[latexpage] [ A . bar{B} ] |
| 9 | NOT A AND B |
[latexpage] [ bar{A }. B ] |
| 10 | NOT AND (NAND) |
[latexpage] [ bar{A . B} ] |
| 11 | A OR B (OR) | A+B |
| 12 | A OR NOT B |
[latexpage] [ A + bar{B} ] |
| 13 | NOT A OR B |
[latexpage] [ bar{A} + B ] |
| 14 | NOT OR (NOR) |
[latexpage] [ bar{A + B} ] |
| 15 | Exclusive-OR |
[latexpage] [ A . bar{B} + bar{A} . B ] |
| 16 | Exclusive-NOR |
[latexpage] [ A . B + bar{A} . bar{B} ] |
مثال شماره 1 قوانین جبر بولی
با استفاده از قوانین فوق، عبارت زیر را ساده کنید: (A + B) (A + C)
Q = (A + B).(A + C)
A.A + A.C + A.B + B.C : قانون توزیع
A + A.C + A.B + B.C : قانون و مستقل (A.A=A)
A (1 + C) + A.B + B.C : قانون توزیع
A.1 + A.B + B.C : قانون یا هویت (1+C=1)
A (1 + B) + B.C : قانون توزیع
A.1 + B.C : قانون یا هویت (1+B=1)
Q = A + (B.C) : قانون و هویت (A.1=A)
سپس عبارت : (A + B) (A + C) همانند قانون توزیع می تواند بهA + (B.C) ساده شود.