فیلتر پایین گذر فعال 

با ترکیب یک مدار فیلتر پایین گذر RC با یک تقویت کننده تفاضلی می‌توان یک مدار فیلتر پایین گذر فعال کامل با تقویت کنندگی بوجود آورد. در آموزش‌های فیلتر غیر فعال RC، دیدیم که یک مدار فیلتر مرتبه اول مانند پایین گذر و فیلترهای بالاگذر می‌توانند تنها با یک مقاومت واحد بصورت سری با یک خازن غیر قطبی متصل به دو سر یک سیگنال ورودی سینوسی ساخته شوند.

فیلتر پایین گذر

همچنین به خاطر داریم که معایب اصلی فیلترهای غیر فعال این است که دامنه سیگنال خروجی کمتر از سیگنال ورودی است یعنی بهره هیچ وقت بزرگتر از یک نیست و برای همین امپدانس بار ویژگی‌های فیلترها را تحت تاثیر قرار می‌دهد.

با مدارهای فیلتر غیر فعال که شامل چندین مراحل هستند، این افت در دامنه سیگنال که “تضعیف” نامیده می‌شود می‌تواند کاملا شدید باشد. یکی از راه های بازیابی یا کنترل این افت سیگنال استفاده از تقویت از طریق استفاده از فیلترهای فعال می‌باشد.

همانطور که از نام آنها پیداست، فیلترهای فعال شامل مولفه‌های فعال مانند تقویت کننده‌های عملیاتی، ترانزیستورها یا FET ها درون طرتحی مدار خود هستند. آنها توان خود را از منبع توان بیرونی می‌کشند و آن را برای تقویت سیگنال خروجی بکار می‌برند.

تقویت فیلتر همچنین می‌تواند برای شکل دهی یا تغییر پاسخ فرکانسی مدار فیلتر با تولید پاسخ خروجی انتخابی‌تر بکار روند که پهنای باند خروجی فیلتر را عریض تر یا حتی باریکتر می‌کند. سپس تفاوت اصلی بین  یک “فیلتر غیر فعال و “یک” فیلتر فعال” تقویت کنندگی آن است.

طراحی فیلتر پایین گذر

یک فیلتر فعال معمولاً از تقویت کننده عملیاتی (op-amp¹) در درون طراحی خود استفاده می‌کند و در آموزش تقویت کننده عملیاتی دیدیم که یک Op-amp دارای امپدانس ورودی بالا، امپدانس خروجی کم و بهره ولتاژ تعیین شده  توسط شبکه مقاومت در داخل حلقه فیدبک  آن است.

برخلاف فیلترهای غیرفعال بالاگذر که از نظر تئوری دارای یک پاسخ فرکانس بالا غیر ذاتی است، حداکثر پاسخ فرکانس یک فیلتر فعال به پهنای باند/ بهره (یا بهره حلقه باز) تقویت کننده عملیاتی مورد استفاده محدود می‌شود. با این وجود، طراحی فیلترهای فعال به طور کلی بسیار آسان تر از فیلترهای غیرفعال است، آنها دارای ویژگی های عملکرد خوب، دقت بسیار خوب با شیب تند و نویز پایین در هنگام استفاده با طراحی مدار خوب هستند.

فیلتر پایین گذر فعال

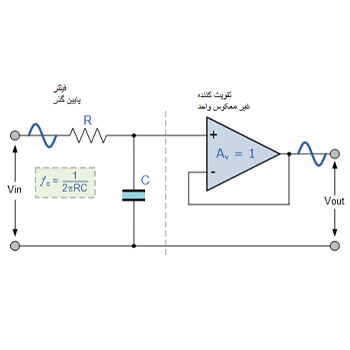
متداول ترین و فعال ترین فیلتر فعال، فیلتر فعال پایین گذر است. اصول عملکرد و پاسخ فرکانس آن دقیقاً مانند فیلتر غیرفعال که قبلاً دیده شده است، تنها تفاوت این بار این است که از یک تقویت کننده عملیاتی برای تقویت و کنترل بهره استفاده می کند. ساده ترین شکل فیلتر فعال پایین گذر اتصال فیلتر معکوس یا غیر معکوس، همان مواردی که در آموزش تقویت کننده عملیاتی بحث شده می باشد، به مدار فیلتر پایین گذر RC اصلی همانطور که نشان داده شده است.

فیلتر پایین گذر مرتبه اول

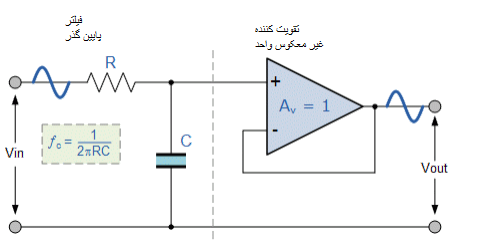
این فیلتر فعال پایین گذر مرتبه اول، شامل یک مرحله فیلتر RC غیر فعال که یک مسیر فرکانسی پایین را به ورودی یک تقویت کننده عملیاتی غیر معکوس فراهم می‌کند است. تقویت کننده بصورت یک دنبال کننده ولتاژ (بافر) که به آن یک بهره DC یک Av = +1 یا بهره واحد که برای فیلتر RC غیر فعال قبلی که دارای بهره DC کمتر از یک نیز بود را ارائه می‌دهد، پیکربندی شده است.

عیب این پیکربندی این است که امپدانس بالای ورودی تقویت کننده‌های عملیاتی از بارگزاری اضافی بر خروجی فیلترها جلوگیری می‌کند درحالی که امپدانس خروجی پایین آن از تاثیر گرفتن نقطه فرکانس قطع فیلترها توسط تغییرات در امپدانس بار جلوگیری می‌کند.

در حالی که این پیکربندی پایداری خوبی را برای فیلتر ایجاد می‌کند، اما نقطه ضعف اصلی آن این است که هیچ بهره ولتاژ بالاتر از یک ندارد. با این حال، اگرچه بهره ولتاژ یکنواخت است، اما بهره توان بسیار زیاد است زیرا امپدانس خروجی آن بسیار کمتر از امپدانس ورودی است. اگر بهره ولتاژ بیشتر از یک مورد نیاز باشد، می توانیم از مدار فیلتر زیر استفاده کنیم.

فیلتر پایین گذر فعال با تقویت کننده

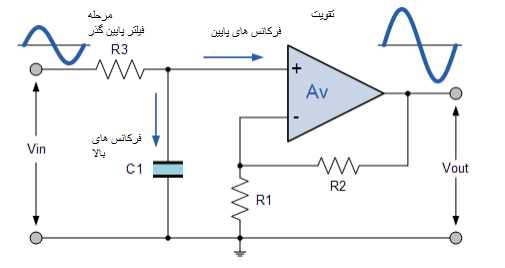
پاسخ فرکانسی مدار همانند فیلتر غیرفعال RC خواهد بود، با این تفاوت که دامنه خروجی با بهره باند گذر A تقویت کننده افزایش می‌یابد. برای یک مدار تقویت کننده غیر معکوس، مقدار بهره ولتاژ برای فیلتر به عنوان تابعی از مقاومت فیدبک (R) تقسیم بر مقدار مقاومت ورودی متناظر آن (R) داده می‌شود و به صورت زیر است:

بهره پاسخ فرکانس مدار همانند فیلتر غیرفعال RC خواهد بود، با این تفاوت که دامنه خروجی با افزایش باند گذر، A تقویت کننده افزایش می‌یابد. برای یک مدار تقویت کننده غیر معکوس، مقدار افزایش ولتاژ برای فیلتر به عنوان تابعی از مقاومت بازخورد (R) تقسیم بر مقدار مقاومت ورودی متناظر آن (R) داده می‌شود و به صورت زیر است:

[latexpage]

[

بهره DC  =left(1+frac{R2}{R1}right)

]

درنتیجه، بهره یک فیلتر پایین گذر فعال بصورت تابع فرکانسی زیر خواهد بود:

بهره فیلتر پایین گذر مرتبه اول

[latexpage]

[

left(AVright)=frac{Vout}{Vin}=frac{A_F}{sqrt{1+{(frac{f}{fc})}^2}}

]

بطوریکه:

Af = بهره باند گذر فیلتر است (1 + R2/R1)

F = فرکانس سیگنال ورودی در واحد هرتز (Hz) است.

Fc = فرکانس قطع در واحد هرتز (Hz) است.

در نتیجه عملیات فیلتر پایین گذر فعال می‌تواند از رابطه بهره فرکانسی بالا بصورت زیر تایید شود:

• در فرکانس بسیار پایین ƒ < ƒc  :

[latexpage]

[

frac{Vout}{Vin}cong A_F

]

• در فرکانس قطع ƒ = ƒc  :

[latexpage]

[

frac{Vout}{Vin}congfrac{A_F}{sqrt2}=0.707A_F

]

• در فرکانس بسیار بالا ƒ > ƒc  :

[latexpage]

[

frac{Vout}{Vin}<A_F

]

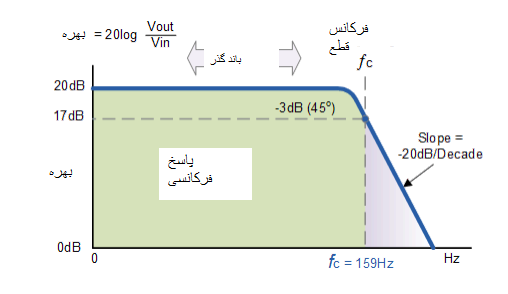
بنابراین، فیلتر فعال پایین گذر دارای یک بهره ثابت A از 0 Hz تا نقطه قطع فرکانس بالا ƒ است. در ƒ بهره 0.707 است و بعد از ƒ با افزایش فرکانس با سرعت ثابت کاهش می‌یابد. یعنی وقتی فرکانس ده برابر شود (یک دهه)،  بهره ولتاژ بر 10 تقسیم می‌ شود.

به عبارت دیگر، هر بار که فرکانس با 10 افزایش یابد، بهره  20 دی بی  (20*(log(10) کاهش می‌یابد. هنگام کار با مدارهای فیلتر، مقدار بهره باند گذر مدار به طور کلی در دسی بل یا dB به صورت تابعی از بهره ولتاژ است و این به عنوان زیر تعریف می شود:

اندازه بهره ولتاژ در واحد (dB)

[latexpage]

[

Avleft(dBright)=20{log}_{10}(frac{Vout}{Vin})

therefore-3dB=20{log}_{10}(0bullet707 frac{Vout}{Vin})

]

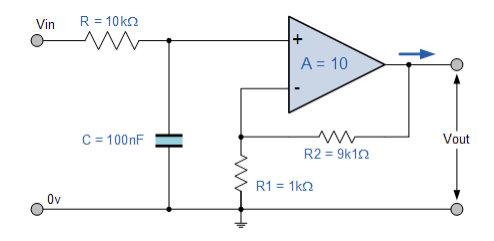
مثال شماره 1 فیلتر پایین گذر فعال

یک مدار فیلتر پایین گذر غیر معکوس طراحی کنید که در فرکانس‌های پایین، در فرکانس قطع بالا یا فرکانس گوشه 159 هرتز و امپدانس ورودی KΩ 10 دارای بهره 10 باشد.

بهره ولتاژ تقویت کننده عملیاتی غیر معکوس بصورت زیر است:

[latexpage]

[

A_f=left(1+frac{R2}{R1}right)=10

]

برای مقاومت R1مقدار 1kΩ را فرض کنید و معادله فوق را برای ارائه مقاومت R2 بصورت زیر مرتب کنید:

[latexpage]

[

R2=left(10-1right)xR1=9 x 1kOmega=9KOmega

]

بنابراین برای بهره ولتاژ 10 ، R1 = 1kΩ و R2 = 9kΩ. با این حال، مقاومت kΩ 9 وجود ندارد بنابراین مقدار ترجیحی 9k1Ω به جای آن استفاده می شود. تبدیل این بهره ولتاژ به یک دسی بل dB معادل مقدار زیر را ارائه می‌دهد:

بهره در dB = 20log A=20log10=20dB

فرکانس قطع یا گوشه (ƒc) به صورت 159Hz با امپدانس ورودی 10kΩ داده می شود. این فرکانس قطع را می توان با استفاده از فرمول زیر یافت:

[latexpage]

[

f_c=frac{1}{2pi RC}Hz , ƒc = 159Hz,R = 10kΩ

]

با آرایش فرمول استاندارد فوق می توان مقدار خازن فیلتر C را بصورت زیر یافت:

[latexpage]

[

C=frac{1}{2pi f_cR}=frac{1}{2pi x 159 x 10kOmega}=100nF

]

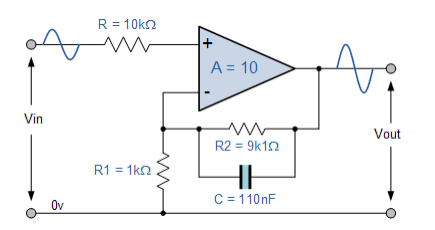
درنتیجه، مدار فیلتر پایین گذر نهایی همراه با پاسخ فرکانسی خود بصورت زیر ارائه شده است:

مدار فیلتر پایین گذر

منحنی پاسخ فرکانسی

اگر امپدانس خارجی متصل به ورودی مدار فیلتر تغییر کند، این تغییر امپدانس بر فرکانس گوشه فیلتر نیز تأثیر می گذارد (اجزای متصل به هم به صورت سری یا موازی). یکی از راه‌های جلوگیری از هرگونه تأثیر خارجی، قرار دادن خازن به موازات مقاومت فیدبک R2 است که به طور موثر آن را از ورودی خارج می‌کند اما همچنان ویژگی‌های فیلتر را حفظ می‌کند.

با این حال، مقدار خازن از 100nF به 110nF کمی تغییر می کند تا مقاومت 9k1Ω را در نظر بگیرد، اما فرمولی که برای محاسبه فرکانس گوشه قطع استفاده می‌شود، همان فرمول مورد استفاده برای فیلتر پایین گذر غیرفعال RC است.

[latexpage]

[

f_c=frac{1}{2pi C R_C}Hz

]

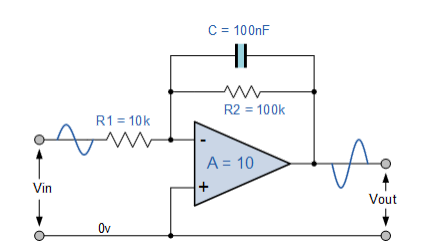
یک مثال از مدار فیلتر پایین گذر فعال بصورت زیر است:

مدار فیلتر تقویت کننده غیرمعکوس ساده شده

مدار فیلتر تقویت کننده معکوس معادل

کاربردهای فیلترهای پایین گذر فعال، در تقویت کننده‌های صوتی، اکولایزرها یا سیستم بلندگوها برای هدایت سیگنال های باس فرکانس پایین به بلندگوهای باس بزرگتر یا کاهش هرگونه نویز فرکانس بالا یا اعوجاج نوع “هیس” است. وقتی از این طریق درکاربردهای صوتی استفاده می‌شود، فیلتر فعال پایین گذر را بعضی اوقات فیلتر “تقویت باس” می‌نامند.

فیلتر پایین گذر فعال مرتبه دوم

همانند فیلتر غیر فعال، یک فیلتر فعال پایین گذر درجه یک می تواند به سادگی با استفاده از یک شبکه RC اضافی در مسیر ورودی، به فیلتر پایین گذر مرتبه دوم تبدیل شود. پاسخ فرکانسی فیلتر پایین گذر مرتبه دوم با نوع مرتبه اول یکسان است با این تفاوت که باند توقف رول آف دو برابر فیلترهای درجه اول با سرعت 40dB/decade (اکتاو/12dB) خواهد بود. بنابراین، مراحل طراحی مورد نیاز فیلتر پایین گذر فعال مرتبه دوم یکسان است.

مدار فیلتر پایین گذر فعال مرتبه دوم

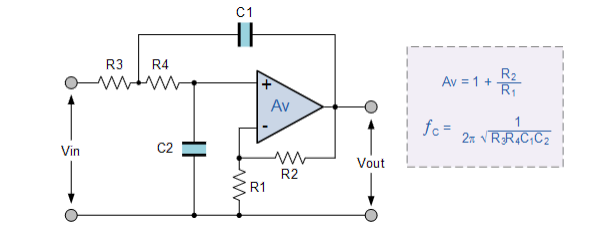
هنگامی که مدارهای فیلتر را با هم سری می‌کنیم و فیلترهای مرتبه بالاتر را تشکیل می‌دهند، بهره کلی فیلتر برابر با حاصل هر مرحله است. به عنوان مثال، بهره یک مرحله ممکن است 10 و بهره مرحله دوم 32 و بهره مرحله سوم 100 باشد. سپس بهره کلی 32000 خواهد بود (10 x 32 x 100) که در زیر نشان داده شده است .

سری کردن بهره ولتاژ

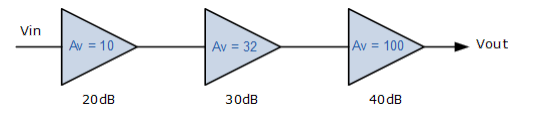
Av=Av1 xAV2 x AV3

AV =10 x 32 x 100 =32,000

AV (dB) =20log₁₀ (32,000)

AV (dB) =90dB

90dB=20dB+30dB+40dB

فیلترهای فعال مرتبه دوم (دو قطبی) مهم هستند زیرا می‌توان با استفاده از آنها فیلترهای مرتبه بالاتر را طراحی کرد. با سری کردن فیلترهای مرتبه اول و دوم، می توان فیلترهایی با مقدار مرتبه، به صورت فرد یا حتی تا بالای هر مقداری می‌توان ساخت. در آموزش بعدی در مورد فیلترها، خواهیم دید که فیلترهای بالا گذر فعال، با وارونه کردن موقعیت های مقاومت و خازن در مدار ساخته می‌شوند.