گفته میشود که سلفها بصورت موازی به یکدیگر وصل شده اند زمانی که هر دو ترمینال آنها متناسبا به هر ترمینال سلف یا سلفهای دیگر وصل شده باشد.
افت ولتاژ دو سر تمامی سلفهای موازی یکسان خواهد بود. سپس، سلفهای موازی دارای یک ولتاژ مشترک در دوسر خود هستند و در مثال ما در زیر ولتاژ دو سر سلفها بصورت زیر است:
…=VL1=VL2=VL3=VAB
در مدار پیش رو سلفهای L1,L2 و L3 همگی به یکدیگر بصورت موازی بین دو نقطه A,B وصل شده اند.
فهرست مطالب
سلف ها در مدار موازی
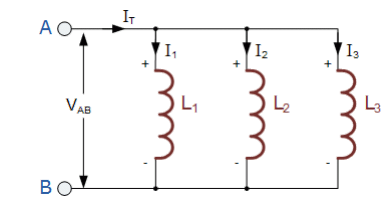

در سلف های سری قبلی دیدیم که ظرفیت القایی کلی LT مدار معادل با مجموع تمامی سلف های مستقل که به یکدیگر اضافه شده اند بود. برای سلف های موازی ظرفیت القایی مدار معادل LT بصورت متفاوت محاسبه شده است.
مجموع جریان های جاری مستقل در هر سلف می تواند با استفاده از قانون جریان کیرشهف (KCL) محاسبه شود بطوریکه : IT=I1+I2+I3 است و از آموزش های قبلی در مورد سلفها می دانیم که نیروی محرکه برگشتی خود القایی در دوسر یک سلف بصورت V=L di/dt ارائه شده است.
سپس با قراردادن مقادیر جریان های مستقل جاری در هر سلف در مدار فوق ما و جایگزینی جریان i برای i1+i2+i3 ، ولتاژ دو سر ترکیب موازی بصورت زیر است:
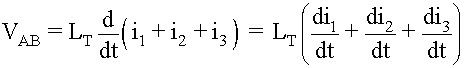
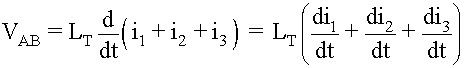
با جایگزینی di/dt در رابطه فوق با v/L داریم:
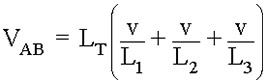
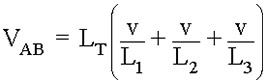
ما میتوانیم برای محاسبه اندوکتانس کل مدار در هنگام اتصال موازی سلفها، آنرا کاهش دهیم و یک رابطه نهایی بصورت زیر ارائه دهیم:
رابطه سلف موازی
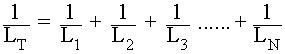
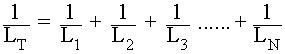
در اینجا، مانند محاسبات برای مقاومتهای موازی، مقدار (u;s (1/Ln اندوکتانس های مستقل به جای خود اندوکتانس ها با هم جمع میشوند. اما باز هم مانند سلفهای متصل به صورت سری، معادله فوق فقط زمانی صادق است که بین دو یا چند سلف القایی متقابل یا اتصال مغناطیسی وجود نداشته باشد (آنها به طور مغناطیسی از یکدیگر جدا شده اند). در مواردی که پیوندی بین سیم پیچ وجود داشته باشد، میزان القای کل همچنین توسط مقدار پیوندی تحت تأثیر قرار میگیرد.
از این روش محاسبه میتوان برای محاسبه هر تعداد القای منفرد متصل به هم در یک شبکه موازی منفرد استفاده کرد. اگر با این وجود، فقط دو سلف منفرد به طور موازی وجود داشته باشد، میتوان از فرمول سادهتر و سریعتر برای یافتن مقدار کل القا استفاده کرد، و این عبارت است از:
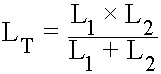
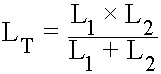
یک نکته مهم که باید در مورد سلفها در مدارهای موازی بخاطر بسپارید، اندوکتانس کل (LT) هر دو یا چند سلف که به طور موازی به یکدیگر متصل می شوند، همیشه کمتر از مقدار کوچکترین القای موجود در زنجیره موازی خواهد بود.
مثال شماره 1 سلف های موازی
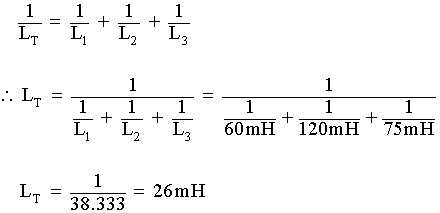
سه سلف 60mH,120mH,75mH به ترتتیب به یکدیگر بصورت موازی بدون القای متقابل بین یکدیگر وصل شده اند. القای کل ترکیب موازی را در واحد میلی هانری بیابید.

سلف های پیوندی متقابل به طور موازی
هنگامی که سلفها به طور موازی به یکدیگر متصل میشوند بنابراین میدان مغناطیسی یکی با دیگری متصل میشود، اثر القا متقابل بسته به مقدار پیوند مغناطیسی بین سیمپیچ ها ، القای کل را افزایش یا کاهش میدهد. تأثیر این القا متقابل به فاصله سیم پیچ ها از یکدیگر و جهت گیری آنها با یکدیگر بستگی دارد.
سلفهای پیوندی متقابل متصل به صورت موازی را میتوان به عنوان “کمک” یا “مخالف” القای کل با کمک سیم پیچ متصل بصورت موازی که القایی معادل کل را افزایش میدهند و سیم پیچهای مخالف موازی که القای کل معادل را کاهش میدهند در مقایسه با سیم پیچ هایی که دارای القا متقابل صفر هستند، طبقه بندی کرد.
سیم پیچ های موازی پیوندی متقابل را می توان به صورت متصل شده بصورت پیکربندی کمکی یا مخالف با استفاده از نقاط قطبیت یا نشانگرهای قطبیت نشان داد که در زیر نشان داده شده است.
سلف های کمکی موازی


ولتاژ دو سر دو سلف کمکی موازی در فوق باید برابر باشند زیرا آنها موازی هستند بنابراین دو جریان i1 و i2 باید تغییر کند بنابراین ولتاژ دوسر آنها باید برابر بماند. سپس القای کل LT برای دو سلف کمکی موازی بصورت زیر است:
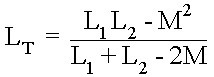
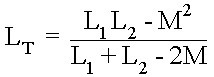
بطوریکه 2M نمایانگر تاثیر سیم پیچ L1 بر روی سیم پیچ L2 و همچنین سیم پیچ L2 بر روی L1 است.
اگر دو القا برابر باشند و پیوند مغناطیسی مانند مدار توروئید کامل باشد، سپس القای معادل دو سلف به صورت موازی L به صورت LT = L1 = L 2 = M است. اگرچه اگر القای متقابل بین آنها صفر باشد، القای معادل L ÷ 2 برابر همان دو سلف خود القای به طور موازی خواهد بود.
اگر یکی از دو سیم پیچ با توجه به دیگری معکوس شود، در این صورت دو سلف مخالف موازی خواهیم داشت و القا متقابل M که بین دو سیم پیچ وجود دارد، به جای اثر کمکی بر روی هر سیم پیچ اثر لغو خواهد داشت، که در زیر نشان داده شده است .
سلف های مخالف موازی
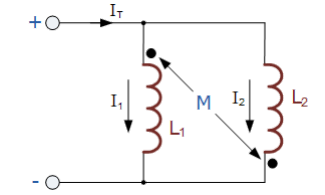

سپس القای کل LT برای دو سلف مخالف موازی بصورت زیر است:
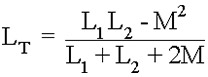
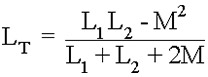
این بار، اگر مقدار این دو القا برابر باشد و پیوند مغناطیسی بین آنها کامل باشد، اندوکتانس معادل و همچنین نیروی محرکه برگشتی خود القایی در دوسر سلفها صفر خواهد بود زیرا که دو سلف اثر یکدیگر را حذف میکنند.
این بدان دلیل است که چون هر دو جریان ، i1,i2 درون هر سلف به نوبت جاری می شود کل شار متقابل تولید شده بین آنها صفر است زیرا دو شار تولید شده توسط هر سلف از نظر اندازه برابر اما در جهت های مخالف هستند.
سپس دو سیم پیچ به طور موثر به شارش جریان به یک اتصال کوتاه در مدار تبدیل میشوند بنابراین اندوکتانس معادل ، LT برابر L ± M) ÷ 2) است.
مثال شماره 2 سلف های موازی
دو سلف که خود القایی آنها 75mH و 55mH است بصورت کمک موازی به یکدیگر وصل شده اند. القای متقابل آنها 22.5mHاست. القای کل ترکیب موازی را بیابید.

مثال شماره 3 سلف های موازی
اندوکتانس معادل مدار القایی زیر را محاسبه کنید.
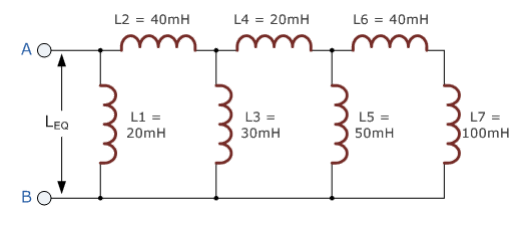

اندوکتانس شاخه اول LA ( سلف L5 بصورت موازی با سلف L6 و L7 است) را محاسبه کنید.

اندوکتانس شاخه دوم LB ( سلف L3 بصورت موازی با سلف L4 و LA است) را محاسبه کنید.

اندوکتانس شاخه دوم LEQ ( سلف L1 بصورت موازی با سلف L2 و LB است) را محاسبه کنید.

سپس اندوکتانس معادل برای مدار فوق بصورت 15mH محاسبه میشود.
خلاصه سلف های موازی
همانند مقاومت، سلفهایی که به طور موازی به یکدیگر متصل میشوند، ولتاژ یکسان V در دو سر خود دارند. همچنین اتصال سلفها به طور موازی باعث کاهش القا مدار موثر با اندوکتانس معادل “N” سلف میشود که به طور موازی به یکدیگر وصل شده اند و برابر عکس جمع عکس های هر اندوکتانس مستقل است.
همانند سلفهای متصل به صورت سری، سلفهای متصل به هم به طور موازی پیوندی متقابل بصورت “کمکی” یا “مخالف” طبقه بندی میشوند، این القا کلی بر اینکه سیمپیچ ها به صورت تجمعی پیوند یافته اند (در همان جهت) یا به طور متفاوت متصل شدهاند (در جهت مخالف) بستگی دارد.
تاکنون ما سلف را به عنوان یک جز منفعل خالص یا ایده آل بررسی کرده ایم. در آموزش بعدی در مورد سلفها، به سلفهای غیر ایده آل که دارای سیمپیچ های مقاوم در دنیای واقعی هستند و مدار معادل یک سلف را به صورت سری با مقاومت تولید میکنند، خواهیم پرداخت و ثابت زمانی چنین مداری را بررسی خواهیم کرد.



